This work is part of my research in computational geometry, where I found a way to make polygonal meshes much smaller. By using my method, the topological information of the mesh can be reduced by 99%, while still being accessible through half-edge queries. You can check out the original publication with more information here ¹.

Intro #

During my PhD, I had to develop a new polygonal mesh generator called Polylla^{2 3 4}. I had to find a data structure that would allow for easy navigation inside a mesh and direct manipulation of its edges. Of all the data structures available, the best one for this purpose was the Half-Edge data structure.

The Half-Edge data structure (also known as the Doubly Connected Edge List (DCEL))⁵ is a useful data structure for navigating inside a polygonal mesh. In this data structure, each edge is explicitly represented as a set of two half-edges, and each face is represented implicitly by the half-edges in its interior. Each half-edge has an orientation, with the interior half-edges of a face having the same orientation (either clockwise or counterclockwise) and the exterior half-edge having the opposite direction.

For example, in the triangulation below, the face with vertices 0-1-2 is represented by the half-edges 4, 5, and 6, all of which have the same orientation inside that face. Their opposite half-edges, the half-edges 0, 9, and 3, respectively, have an opposite direction. (The orientation of the faces is clockwise in the image as it is part of research that uses this orientation, but in computer graphics, the most common orientation is counterclockwise).

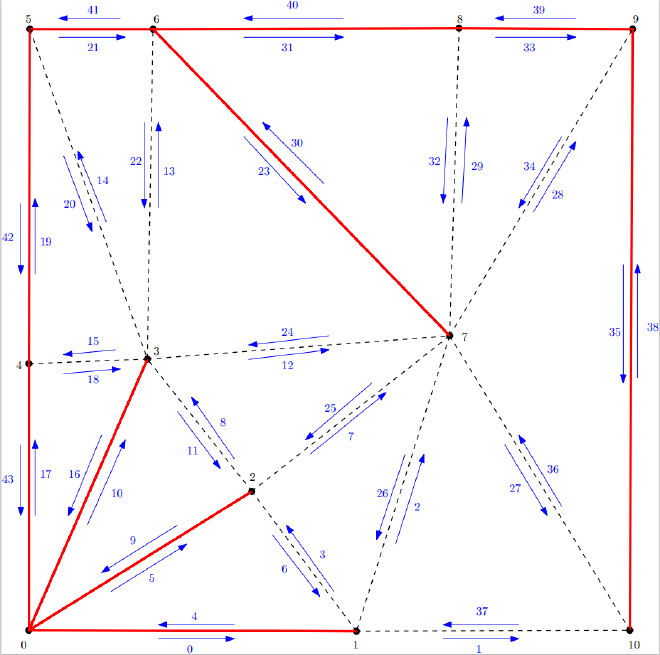
Half-edge queries #

To navigate inside a mesh, we have a set of queries. Given a half-edge \(e\), the primitive queries⁶ supported by the data structure are the following (see Figure 1):

• twin(e) return the opposite half-edge of \(e\)
• next(e): return the half-edge next to \(e\) inside the same face in counter-clockwise order.
• prev(e): return the half-edge previous to \(e\) inside the same face in counter-clockwise order.
• origin(e): return the source vertex of the half-edge \(e\).
• target(e): return the target vertex of the half-edge \(e\).
• face(e): return the index of the incident face to the half-edge \(e\).

It is common to extend those queries according to the necessities of the problem to solve, in my case, I extended the half-edge with the following queries:

• CW_edge_to_vertex(e): return the half-edge with source vertex \(origin(e)\) and next to \(e\) in clockwise.
• CCW_edge_to_vertex(e): return the half-edge with source vertex \(origin(e)\) and previous to \(e\) in counter-clockwise.
• isBorder(e): return true if half-edge \(e\) is incident to the outer face of the mesh.
• length(e): return the length of the half-edge \(e\).
• edgeOfVertex(v): return an arbitrary half-edge with source vertex \(v\).
• incidentHalfEdge(f): return an arbitrary half-edge delimiting face \(f\).
• degree(v): return the number of the edges incident to with source vertex \(v\).

In some literature, CCW_edge_to_vertex(e) and CW_edge_to_vertex(e) are called \(next_v\) and \(prev_v\).

Before we can begin with the implementation, we first need a file format to read a mesh. We have chosen the common file format for 2D meshes, an OFF file.

Input file (OFF) #

An OFF file is a common format for store a mesh, developed for the software Geomview⁷, and it is still used for modern software as Meshlab⁸ and Paraview⁹. If you want to generate a polygonal mesh in OFF format from a point set, you can use Triangle¹⁰ with the command -g

This format stores a polygonal mesh as a set of vertices and faces. The triangulation shown above, when stored in OFF format, appears as follows:

OFF
11  12  22
 0  0  0
 5434.9668391472287  0  0
 1934.3633489238321  4501.0628511691029  0
 0  10000  0
 0  4430.4242110758132  0
 7177.2771157039515  10000  0
 2082.4882032210944  10000  0
 3703.7846356429982  2339.6091203110768  0
 10000  10000  0
 10000  0  0
 6988.9064005448017  4883.8440215972032  0
 3      4     0     2
 3      3     2     6
 3      2     3     4
 3      6     2    10
 3      0     7     2
 3     10     7     1
 3      1     7     0
 3     10     1     9
 3     10     8     5
 3      8    10     9
 3      5     6    10
 3     10     2     7

The following 11 lines represent the vertices of the triangulation, with each vertex having an implicit index starting from 0. The next 12 lines correspond to the faces of the triangulation. The first number indicates the number of vertices of each face, followed by the next 3 numbers that represent the vertices of a face, represented by their implicit index, in counterclockwise order.

Implementation #

Now, we have the basic concepts to implement the half-edge data structure. So basically, we just need implement 3 things

1. Define struct and classes
2. Read the off file
3. Construct interior and exterior half-edges
4. Half-edge queries

This implementation is based in modern C++, so you will see several vector, access of memory using .at, pairs, etc.

Array of struct (AoS) and the Triangulation Class #

To store the half-edge data structure, we will use two Array of Structs (AoS). This data structure has the advantage of storing all the structs in continuous memory, making it fast to access the elements. We define two structs: one for vertices and the other for half-edges.

struct vertex{
    double x;
    double y;
    bool is_border = false; // if the vertex is on the boundary
    int incident_halfedge; // halfedge incident to the vertex, vertex is the origin of the halfedge
};

struct halfEdge {
    int origin; //tail of edge
    int twin; //opposite halfedge
    int next; //next halfedge of the same face
    int prev; //previous halfedge of the same face
    int is_border; //1 if the halfedge is on the boundary, 0 otherwise
};

We define the triangulation as a class. This class will contain an AoS of vertices, called Vertices, and an AoS of half-edges, called HalfEdges, as private attributes, and the queries showed before as methods of the class.

class Triangulation 
{
private:
    //Statically data
    int n_halfedges = 0; //number of halfedges
    int n_faces = 0; //number of faces
    int n_vertices = 0; //number of vertices
    int n_border_edges = 0; //number of border edges
    double t_triangulation_generation = 0; //time to generate the triangulation

    std::vector<vertex> Vertices; //AoS of vertices
    std::vector<halfEdge> HalfEdges; //AoS of half-edges
public:
	int n_faces();
	int n_halfEdges();
	int n_vertices();
	
	int next(int e);
	int origin(int e);
	int target(int e);
	int twin(int e);
	int prev(int e);
	int edge_of_vertex(int v); 

	int CCW_edge_to_vertex(int e);
	int CW_edge_to_vertex(int e);
	
	bool is_interior_face(int e);
	bool is_border_vertex(int v);
	int degree(int v);
	int incident_halfedge(int f);
}

Now we will implement our public methods. Our first public method is the constructor

Triangulation(std::string OFF_file){
    std::cout<<"Reading OFF file "<<OFF_file<<std::endl;
    std::vector<int> faces = read_OFFfile(OFF_file);
    construct_interior_halfEdges_from_faces(faces);
    construct_exterior_halfEdges();
}	

This constructor read an OFF file to fulfill the vector Vertices and an auxiliary array faces, we will use both vector to construct the interior and the exterior half-edges.

Read OFF file #

To read the OFF file, we define an auxiliary function ¹¹ that checks whether a line only contains white space.

We define the method read_OFFfile that receives a string with the name of the OFF file. We open that file and check if the first line is labeled as an OFF file. If it is true, we read the file line by line. For each line, we check if it is a comment (starts with “#”) or white space. To read the lines, we use istringstream, which allows us to stream each value of a line separated by white spaces.

After checking the number of vertices and faces in the triangulation, we reserve memory space to use. We use the reserve method ¹² because it allows us to request memory without changing the size of elements in the vector or constructing elements, so we can use the push_back method to add elements instead of indices.

The vertices are stored in the Vertices vector. We only store the coordinates of each vertex because the OFF file does not provide information about whether a vertex is a border and its incident edges.

The faces are stored in the faces vector. We ignore the first element that indicates the length of the polygon (as we know that it is 3). faces stores the indices of the vertices previously allocated in Vertices. Each three vertices represent a new face.

//https://stackoverflow.com/a/22395635
// Returns false if the string contains any non-whitespace characters
// Returns false if the string contains any non-ASCII characters
bool isWhitespace(std::string s){
    for(int index = 0; index < s.length(); index++)
        if(!std::isspace(s[index]))
            return false;
    return true;
}

//Read the mesh from a file in OFF format
std::vector<int> read_OFFfile(std::string name){
    //Read the OFF file
    std::vector<int> faces;
    std::string line;
    std::ifstream offfile(name);
    double a1, a2, a3;
    std::string tmp;
    if (offfile.is_open()){
        //Check first line is a OFF file
        while (std::getline(offfile, line)){ //add check boundary vertices flag
            std::istringstream(line) >> tmp;
            if (tmp[0] != '#' && !isWhitespace(line))
            {
                if(tmp[0] == 'O' && tmp[1] == 'F' && tmp[2] == 'F') //Check if the format is OFF
                    break;
                else{
                    std::cout<<"The file is not an OFF file"<<std::endl;
                    exit(0);
                }
            }
        }
        //Read the number of vertices and faces
        while (std::getline(offfile, line)){ //add check boundary vertices flag
            std::istringstream(line) >> tmp;
            if (tmp[0] != '#' && !isWhitespace(line))
            { 
                        std::istringstream(line) >> this->n_vertices >> this->n_faces;
                        this->Vertices.reserve(this->n_vertices);
                        faces.reserve(3*this->n_faces);
                        break;
                        
            }
        }
        //Read vertices
        int index = 0;
        while (index < n_vertices && std::getline(offfile, line) ){
            std::istringstream(line) >> tmp;
            if (tmp[0] != '#' && !isWhitespace(line))
            {
                std::istringstream(line) >> a1 >> a2 >> a3;
                vertex ve;
                ve.x =  a1;
                ve.y =  a2;
                this->Vertices.push_back(ve);
                index++;
            }
        }
        //Read faces
        int lenght, t1, t2, t3;
        index = 0;
        while (index < n_faces && std::getline(offfile, line)){
            std::istringstream(line) >> tmp;
            if (tmp[0] != '#' && !isWhitespace(line))
            {
                std::istringstream(line) >> lenght >> t1 >> t2 >> t3;
                faces.push_back(t1);
                faces.push_back(t2);
                faces.push_back(t3);
                index++;
            }
        }

    }
    else 
            std::cout << "Unable to open node file"; 
    offfile.close();
    return faces;
}

Once we read the OFF file, we have two vectors, with the information that we need to next phase.

Construct interior half-edges #

This is an important part of the article. We will convert each face of the mesh into three half-edges. As each face is represented by vertices \(v_1\), \(v_2\), and \(v_3\), we can generate three half-edges using them: the half-edges \(v_1 - v_2\), \(v_{2} - v_{3}\), and \(v_3 - v_1\).

For each face \(f_i\) in faces, and for each vertex \(v_j \in f_{i}\), we create a new half-edge \(h_{i}\) that defines the vertex \(v_j\) as the origin and the vertex \(v_{j+1}\) as the target. We use modular arithmetic to avoid selecting a vertex from the next face \(f_{i+1}\). We know that the next half-edge is \(h_{i+1}\), and the previous half-edge is \(h_{i+2}\). Since this is a triangle, the query next(next(h_i)) = prev(h_i) holds. These half-edges may not be created yet, but we can define their indices anyway.

All of the half-edges that we are generating are interior half-edges. Since we don’t have information about the border, we set is_border = false. We also don’t have information about the twin half-edge, so we set the twin as -1 to mark the half-edges that still don’t have a twin.

To search for the twin, we define a hash table of pairs \(\mathcal{H}\), which is called map_edges in the code, and we define the lambda function hash_for_pair. For each new half-edge \(h_i\) that we create, we add its origin and target as a pair in the hash table. When all of the half-edges are created, we iterate over the vector of half-edges, and we search for the index of the half-edge \(h_j\) that contains the origin and target in the other way around of \(h_i\). That half-edge \(h_j\) is the twin half-edge \(h_i\), and we set \(h_j.twin = i\) and \(h_i.twin = j\).

In that last iteration, we can also discover which half-edge is a border half-edge. If a half-edge has no twin, then we label it and its vertices as a border half-edge and border vertices.

//Generate interior halfedges using a a vector with the faces of the triangulation
//if an interior half-edge is border, it is mark as border-edge
//mark border-edges
void construct_interior_halfEdges_from_faces(std::vector<int> &faces){
    auto hash_for_pair = [](const std::pair<int, int>& p) {
        return std::hash<int>{}(p.first) ^ std::hash<int>{}(p.second);
    };
    std::unordered_map<_edge, int, decltype(hash_for_pair)> map_edges(3*this->n_faces, hash_for_pair); //set of edges to calculate the boundary and twin edges
    for(std::size_t i = 0; i < n_faces; i++){
        for(std::size_t j = 0; j < 3; j++){
            halfEdge he;
            int v_origin = faces.at(3*i+j);
            int v_target = faces.at(3*i+(j+1)%3);
            he.origin = v_origin;
            he.next = i*3+(j+1)%3;
            he.prev = i*3+(j+2)%3;
            he.is_border = false;
            he.twin = -1;
            Vertices.at(v_origin).incident_halfedge = i*3+j;
            map_edges[std::make_pair(v_origin, v_target)] = i*3+j;
            HalfEdges.push_back(he);
        }
    }
    
    //Calculate twin halfedge and boundary halfedges from set_edges
    std::unordered_map<_edge,int, decltype(hash_for_pair)>::iterator it;
    for(std::size_t i = 0; i < HalfEdges.size(); i++){
        //if halfedge has no twin
        if(HalfEdges.at(i).twin == -1){
            int tgt = origin(next(i));
            int org = origin(i);
            std::pair<int,int> twin = std::make_pair(tgt, org);
            it=map_edges.find(twin);
            //if twin is found
            if(it!=map_edges.end()){
                int index_twin = it->second;
                HalfEdges.at(i).twin = index_twin;
                HalfEdges.at(index_twin).twin = i;
            }else{ //if twin is not found and halfedge is on the boundary
                HalfEdges.at(i).is_border = true;
                Vertices.at(org).is_border = true;
                Vertices.at(tgt).is_border = true;
            }
        }
    }
}

Construct exterior half-edges #

Since each face only provides us with information on its interior half-edges, we need to construct the exterior half-edges after creating them.

For each border interior half-edge \(h_i\) that we created, we generate a new half-edge \(h_j\) such that \(h_j.origin = h_i.target\), \(h_j.twin = i\), and \(h_i.twin = j\). We remove the border label of \(h_i\) and add \(h_j\) at the end of the HalfEdges vector, so the index of \(j\) is equal to the length of the half-edge vector.

The new border half-edges do not yet have their next and prev edges. To solve this problem, we take advantage of the fact that our mesh is a triangulation and use the operations CCW_edge_to_vertex() and CW_edge_to_vertex() to search for their indices. To find the next of each border half-edge \(h_i\), we continuously apply the CCW_edge_to_vertex() operation on \(h_i.twin()\) until we get the index of a new border half-edge, which is the next of \(h_i\). Similarly, to search for the prev, we iterate through the CW_edge_to_vertex() operation until we find a half-edge whose twin is a border-edge.

//Generate exterior halfedges
//This takes  n + k time where n is the number of vertices and k is the number of border edges
void construct_exterior_halfEdges(){
    //search interior edges labed as border, generates exterior edges
    //with the origin and target inverted and add at the of HalfEdges vector
    //std::cout<<"Size vector: "<<HalfEdges.size()<<std::endl;
    this->n_halfedges = HalfEdges.size();
    for(std::size_t i = 0; i < this->n_halfedges; i++){
        if(HalfEdges.at(i).is_border){
            halfEdge he_aux;
            he_aux.twin = i;
            he_aux.origin = origin(next(i));
            he_aux.is_border = true;
            HalfEdges.at(i).is_border = false;
            
            HalfEdges.push_back(he_aux);
            HalfEdges.at(i).twin = HalfEdges.size() - 1 ;
        }    
    }
    //traverse the exterior edges and search their next prev halfedge
    int nxtCCW, prvCCW;
    for(std::size_t i = n_halfedges; i < HalfEdges.size(); i++){
        if(HalfEdges.at(i).is_border){
            nxtCCW = CCW_edge_to_vertex(HalfEdges.at(i).twin);
            while (HalfEdges.at(nxtCCW).is_border != true)
                nxtCCW = this->CCW_edge_to_vertex(nxtCCW);
            HalfEdges.at(i).next = nxtCCW;

            prvCCW = this->next(twin(i));
            while (HalfEdges.at(HalfEdges.at(prvCCW).twin).is_border != true)
                prvCCW = this->CW_edge_to_vertex(prvCCW);
            HalfEdges.at(i).prev = HalfEdges.at(prvCCW).twin;
        }
    }
    this->n_halfedges = HalfEdges.size();
}

Implemetantion of queries #

We now have a polygonal mesh stored using the half-edge data structure. All that is left to do is to define the queries showed before. These queries require the index of a half-edge, face, or vertex to retrieve information.

The most basic queries are those that can be obtained by simply consulting the attributes of the data structures. These queries include origin, target, twin, next, prev, is_border_face for the half-edge struct, and get_PointX, get_PointY, edge_of_vertex for the Vertex struct.

//Calculates the tail vertex of the edge e
//Input: e is the edge
//Output: the tail vertex v of the edge e
int origin(int e){
    return HalfEdges.at(e).origin;
}


//Calculates the head vertex of the edge e
//Input: e is the edge
//Output: the head vertex v of the edge e
int target(int e){
    return this->origin(HalfEdges.at(e).twin);
}

//Return the twin edge of the edge e
//Input: e is the edge
//Output: the twin edge of e
int twin(int e){
    return HalfEdges.at(e).twin;
}

//Calculates the next edge of the face incident to edge e
//Input: e is the edge
//Output: the next edge of the face incident to e
int next(int e){
    return HalfEdges.at(e).next;
}


//Return the twin edge of the edge e
//Input: e is the edge
//Output: the twin edge of e
int prev(int e){
    return HalfEdges.at(e).prev;
}

//Input: edge e
//Output: true if is the face of e is border face
//        false otherwise
bool is_border_face(int e){
    return HalfEdges.at(e).is_border;
}

//return the x coordinate of the vertex v
double get_PointX(int v){
   return Vertices.at(i).x;
}
//return the y coordinate of the vertex v
double get_PointY(int v){
   return Vertices.at(i).y;
}

//return a edge associate to the node v
//Input: v is the node
//Output: the edge associate to the node v
int edge_of_vertex(int v){
	return Vertices.at(v).incident_halfedge;
}

We can create more complex queries, taking advantage of the topology of the mesh, and using the basic queries to built them.

For example the queries CCW_edge_to_vertex and CW_edge_to_vertex, take advantage that each face is a triangle to get implement the query. Both can be defined as

• CCW_edge_to_vertex(e): twin(prev(e))
• CW_edge_to_vertex(e): next(twin(e))

And they are implemented as:

//Given a edge with vertex origin v, return the next coutnerclockwise edge of v with v as origin
//Input: e is the edge
//Output: the next counterclockwise edge of v
int CCW_edge_to_vertex(int e){
    int twn, prv;
    prv = HalfEdges.at(e).prev;
    twn = HalfEdges.at(prv).twin;
    return twn;
}    

//Given a edge with vertex origin v, return the prev clockwise edge of v with v as origin
//Input: e is the edge
//Output: the prev clockwise edge of v
int CW_edge_to_vertex(int e){
    int twn, nxt;
    twn = HalfEdges.at(e).twin;
    nxt = HalfEdges.at(twn).next;
    return nxt;
}    

The query degree(v) is constructed using the query edge_of_vertex(v) to get and incident half-edge \(h_i\) to the vertex \(v\), with \(h_i.origin = v\), and the query nextCCW(e) to circle around \(v\), n-times, until back to the original \(h_i\).

//Calculates the number 
int degree(int v){
    int e_curr = edge_of_vertex(v);
    int e_next = CCW_edge_to_vertex(e_curr);
    int adv = 1;
    while (e_next != e_curr)
    {
        e_next = CCW_edge_to_vertex(e_next);
        adv++;
    }
    return adv;
}

The query to get an incident half-edge to a face \(f\) also takes advangate that each face is a triangulation. As we created the half-edge in consecutive order, each 3 half-edge in the vector Half-edges is a new face. So we can implement incident_halfedge as:

int incident_halfedge(int f){
    return 3*f;
}

More queries can be defined in the same way according to the necessities of the problem.

Conclusions #

I have shown you the basics of how to construct the half-edge data structure in C++. This implementation is useful if you have an immutable mesh and need to navigate inside it.

However, this implementation lacks operations such as point insertion and edge deletion. Additionally, it only works for triangulations, and if you have polygons of arbitrary shape, you will need to modify the construction of interior half-edges to accept polygons with more than three edges (which involves nested iteration).

If you need to work with large meshes and encounter memory problems, you can check out my new research on a novel compact half-edge data structure here ¹³.

This work was published in the SIAM IRM conference 2023, you can see the paper here¹

References #