[ Principal | Integrantes | Estado de Avance | Resultados | Instrucciones de Uso | Archivos ]
![]()

![]()
Una vez terminado este proyecto, estamos en posición de sacar algunas conclusiones respecto a los temas que fueron tratados durante este, a los problemas que fueron enfrentados y a las herramientas o ideas que se utilizaron para resolverlos.
Nuestro proyecto puede dividirse en dos grandes tareas, por un lado estaba el implementar la maquinaria matemática necesaria para realizar la simulación física, tarea que incluye el diseñar algoritmos eficientes para resolver las ecuaciones (que en su mayoría son ecuaciones diferenciales de segundo orden) que aparecen al plantear un sistema regido por las leyes de Newton. Por otro lado, estaba el realizar la implementación gráfica de este sistema, es decir, realizar una presentación en pantalla realista del sistema que se quiere simular, en este punto se utilizaron cosas como perspectiva, texturas, iluminación, etc.
Respecto del primer punto, con relación a los algoritmos matemáticos, se realizó una primera implementación en la cual para resolver las ecuaciones diferenciales se realizaban expansiones de Taylor a primer orden. De esta manera, se obtienen ecuaciones del tipo:
aceleración= Suma(fuerza entre i y j);
Velocidad= velocidad + aceleración*d(tiempo);
Posicion=posicion+ velocidad*d(tiempo);
Como se ve, esta es una expansión a primer orden, lo que trae como consecuencia que si la variación de tiempo entre una iteración y la siguiente es grande (o no es lo suficientemente chica) entonces se empiezan a generar errores, los que se manifiestan en el sistema como una pérdidad de energía en el sistema, es decir, es una especie de "roce numérico".
Para solucionar este problema, se debió cambiar el algoritmo, implementándose el algoritmo de Runge-Kutta, el que permite resolver un sistema de ecuaciones de primer grado con una precisión mucho mayor que el algoritmo anterior (es una aproximación de tercer orden). Ahora, en nuestro caso, tenemos sistemas de ecuaciones de segundo grado, en el cual hay que resolver tres ecuaciónes por cada partícula (una por cada dimensión), es decir, tenemos un sistema de 3*n ecuaciónes de segundo grado, donde n es el número de partículas. Sin embargo, y para poder utilizar el método de Runge-Kutta, existe una herramienta física, conocida como las ecuaciones de Euler-Lagrange, que permite transformar una ecuación a derivadas parciales de segundo orden en dos ecuaciones de primer orden. De esta manera, podemos transformar nuestro sistema de 3*n ecuaciones de segundo orden en 6*n ecuaciones diferenciales de primer orden (son 3*n ecuaciones para la posición en función de la velocidad y 3*n ecuaciones para la velocidad en función de la aceleración). Entonces, podemos utilizar el método de Runge-Kutta para resolver el sistema, lo que aumenta notablemente la precisión de la simulación y reduce drásticamente el "roce numérico". Sin embargo, una vez realizadas ambas implementaciones vimos que debido a que aumenta notablemente el número de cálculos necesarios para utilizar el método de Runge-Kutta, es preferible utilizar el primer algoritmo a primer orden, pero reduciendo el tamaño de los pasos, y de esta manera se logra un funcionamiento más rápido con la misma precisión.
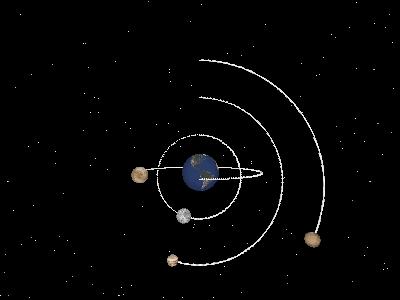
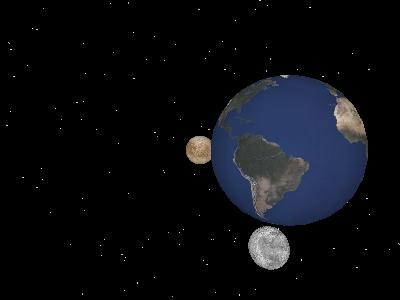
Respecto del problema gráfico, se utilizaron diferentes técnicas para realizar una simulación más realista. Entre estas técnicas encontramos la utilización de texturas, la visión en perspectiva, fuentes de luz dinámicas y finalmente la posibilidad de cambiar el punto de vista de la simulación. Cabe destacar la implementación de las colas, que permite seguir la trayectoria de un objeto celeste a través de la creación de una estela detrás del cuerpo.
Además, una nueva característica permite utilizar una cámara que vaya "persiguiendo" al planeta por detrás. Esto se logró situando el punto de vista en un punto arbitrario, seleccionable por el usuario, de la cola del planeta, y poniendo en el centro de la visión al planeta es su ubicación actual.
Junto con todo esto, y con el fin de mejorar el realismo de la simulación, se añadió un fondo de estrellas, las cuales no son más que esferas de radio muy pequeño localizadas lejos del observador, en posiciones elegidas al azar en tiempo de ejecución.