Curso CC20A - Variables de estado

1.3.2. Propiedades de las variables de estado

Podemos ver ahora cómo el computador puede realizar los cálculos necesarios para ejecutar una simulación de manera iterativa. Suponga que queremos calcular los valores de las variables descriptivas y'₁, y'₂, ..., y'_n en t', dados los valores de y₁, y₂, ..., y_m en t. Suponga que las reglas de interacción pueden ser traducidas a un programa computacional, el cual, para un conjunto finito de tiempos t₁, t₂, t₃, ..., t_i, t_i+1, ..., puede hacer lo siguiente.

Dado cualquier conjunto de valores de estado yⁱ₁, ..., yⁱ_m en t_i, el programa calcula los valores únicos yⁱ⁺¹₁, ..., yⁱ⁺¹_m+1, ..., yⁱ⁺¹_n en t_i+1 especificados por las reglas de interacción. Cuando esto sucede, decimos que el programa puede calcular o simular la transición del modelo de t_i a t_i+1.

El conjunto {t₁, t₂, ...} es llamado tiempos computacionales. Son los tiempos del modelo en los cuales el programa puede producir el conjunto de valores de descripción del modelo. Algunas veces estos tiempos son múltiplos sucesivos de algún tiempo h, por lo que t_i+1 - t_i = h. Esto es llamado una simulación de tiempo discreto. Se supone que las reglas de interacción no dependen del tiempo, sólo de los valores de estado y₁, ..., y_m. El modelo es llamado invariante en el tiempo.

Imagime que la simulación de un modelo bien definido es llevada a cabo por un programa que tiene acceso a las variables descriptivas a₁, a₂, a₃, ..., a_n. Las siguientes propiedades explican el concepto de estado.

Inicialización del programa

₁

2. Repetir una ejecución. Suponga que queremos repetir el cálculo de los valores y'₁, ..., y'_n en t' dados los valores y₁, ..., y_n en t, por ejemplo porque perdimos algún resultado de la primera ejecución de la simulación. Las dos ejecuciones pueden ser hechas en diferentes computadoras en diferentes tiempos, y aún así los resultados van a ser los mismos, dados los mismos valores iniciales y₁, ..., y_m.

3. Interrupción del programa y re-inicio. Suponga que después de calcular los valores y'₁, ..., y'_n en t' se interrumpe el programa. El programa debe ser capaz de re-iniciar desde el mismo punto en el cual fue detenido, y debe calcular los mismos valores finales. Para esto basta guardar los valores asociados a a₁, a₂, a₃, ..., a_m en el momento en que se interrumpió el programa.

4. Recuperación del programa. Suponga que ocurre una falla en el computador mientras el programa está siendo ejecutado. Cuando la falla es reparada, se quiere seguir con la simulación, pero se quiere evitar re-inicializar el programa desde el estado inicial. La re-inicialización del programa debería obtener el mismo resultado si ésta se hace desde el inicio o desde el punto en que ocurrió la falla.

Procedimiento prototipo para simulación de tiempo discreto de modelos invariantes en el tiempo

Si se trata de calcular las variables de estado y₁, ..., y_n para instantes t = t_M, t_M+1, ..., t_M+N (con t_i+1 = t + h) y además las reglas no dependen del tiempo, sino sólo del estado anterior, estamos frente a un caso que llamaremos de tiempo discreto e invariante en el tiempo. El siguiente sería un plan a seguir para implementar un programa de simulación para estos casos.

₁

₂

₃

₁

₂

₃

2. Inicializar el reloj en t_M.

3. Aplicar las reglas de interacción al contenido de las variables de estado actuales para producir los valores correspondientes al siguiente estado. Calcular a partir de las variables de estado el resto de las variables descriptivas.

4. Avanzar el reloj en la unidad de tiempo h especificada en el modelo.

5. Ver si el reloj excedió el tiempo de simulación (t_M + Nh). Si excedió el tiempo, termina, si no, vuelve a 3.

Ejemplo:

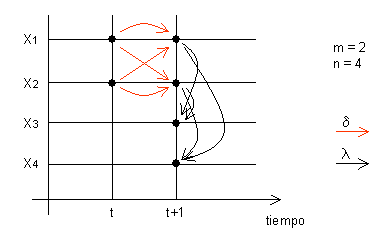
La siguiente figura muestra el proceso de aplicar el paso 3. Los puntos rojos indican las variables de estado, y los puntos azules las variables descriptivas. A partir de las variables de estado es posible obtener las variables descriptivas para todos los tiempos siguientes.

Especificación formal de modelos

El paso 3 se puede ver como un subprograma que acepta una lista de valores de estado y entrega una lista de variables descriptivas actualizada. Este subprograma puede verse como una función (en sentido matemático) f cuyo dominio es el conjunto de todos los valores posibles de las variables de estado y como rango el conjunto de los valores posibles de todas las variables descriptivas, es decir:

₁

_m+1

donde y₁, ..., y_m son los valores de las variables de estado y y'₁, ..., y'_m, y'_m+1, ..., y'_n son los valores de las variables descriptivas una unidad de tiempo después.

Podemos decir que f está constituída de dos funciones:

₁

_m+1

donde:

₁

l(y'₁, ..., y'_m) = (y'₁, ..., y'_n)

f(y₁, ..., y_m) = l(d(y₁, ..., y_m))

Nótese que la función d no es instantánea, es decir, los valores y'₁, ..., y'_m son en el instante t+1 (si y₁, ..., y_m en t) y también y'₁, ..., y'_n (la salida de la función l) son en ese mismo instante t+1.

d toma el estado en que se encuentra el modelo en el instante actual y produce el estado en el que estará el modelo en el próximo instante de cálculo. d se llama la función de transición de estados, o más corto, la función de transición.

l toma el estado del modelo en un instante dado y produce la descripción total del modelo en ese estado. l se llama función de salida.

En la práctica, podemos estar interesados en observar sólo algunas de las variables descriptivas (no todas), las que se denominan variables de salida. Se puede modificar la función l de modo que produzca los valores de las variables de salida (que son una descripción parcial del modelo en su estado actual).

Formalicemos los estados y las salidas:

Sea VARIABLES el conjunto de variables descriptivas, VARIABLES·ESTADO el conjunto de las variables de estado, y VARIABLES·SALIDA el conjunto de variables de salida. Entonces:

Sea m el número de variables de estado. Entonces un estado del modelo es una tupla (y₁, ..., y_m) donde cada y_i es un valor en el rango de la variable de estado i-ésima. El conjunto de todas estas tuplas se denomina ESTADOS.

Formalmente, se define como:

_{b
Î VARIABLES·ESTADO}

Similarmente, si hay p variables de salida, una salida del modelo es una tupla (y₁, ..., y_p), donde cada y_j es un valor en el rango de la variable de salida j-ésima. El conjunto de todas estas tuplas se denomina el conjunto de SALIDAS.

Formalmente, se define como:

_{g
Î VARIABLES·SALIDA}

Con estas definiciones entonces:

Podemos interpretar esto de la siguiente forma: si ESTADO es el estado del modelo en el instante t, entonces d(ESTADO) es el estado del modelo en t+1, y l(ESTADO) es la salida del modelo en el instante t.

Ejemplo: (caso de los trenes)

Habíamos visto que RAPIDO y EXPRESO (la ubicación de los trenes) eran un conjunto de variables de estado. El rango de cada una de estas variables es HITOS. Luego:

ESTADOS = HITOS x HITOS y un ESTADO típico tiene la forma (r,e) donde r Î HITOS y e Î HITOS.

También vimos cómo calcular el estado en t+1 dado el estado en t. Escribamos la función de transición:

tal que para cada (r,e) Î ESTADOS:

d(r,e) = (r + D(e - r), e + D(r - e))

porque r + D(e - r) es la ubicación del rápido en t+1 y e + D(r - e) es la ubicación del expreso en t+1.

Supongamos ahora que elegimos como variables de salida las lecturas de las señales que pueden hacerse en los hitos L y -L (los extremos del ferrocarril). Las variables de salida son entonces:

Ya que cada una de estas variables tiene rango {-1,1}, tenemos que:

SALIDAS = {-1,1} x {-1,1} x {-1,1} x {-1,1} También habíamos calculado las lecturas de las señales en cualquier punto P en t, y que eran completamente determinadas por las ubicaciones de RAPIDO y EXPRESO en t. Así, podemos especificar d:

Por tanto, tomando en cuenta esos cálculos, para todo (r,e) Î ESTADOS:

[anterior][home][siguiente]