[anterior]
[home]
[siguiente]
1.3.1. Ejemplo 6 - Sistema de trenes
Los maquinistas de dos trenes, el "rápido" y el "expreso" están tratando de llegar a un punto común para traspasar una carga. Cada tren corre sobre sus propios rieles, paralelos a los del otro. Los trenes disponen de un sistema simple de comunicación que permite detectar si el otro tren está hacia adelante o hacia atrás. El ferrocarril corre entre -L y L, y hay hitos en los cuales se activa el sistema de comunicación (hay un total de 2L + 1 hitos).
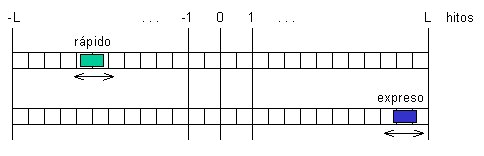 Podemos simplificar la figura anterior de la siguiente manera:
Podemos simplificar la figura anterior de la siguiente manera:
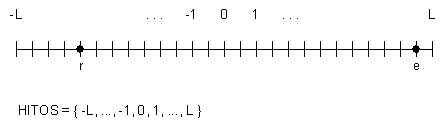 Descripción
Descripción
Componentes
TREN·RAPIDO, TREN·EXPRESO, HITOS.
Variables descriptivas
TREN·RAPIDO
RAPIDO - con rango HITOS; describe la ubicación del TREN·RAPIDO.
TREN·EXPRESO
EXPRESO - con rango HITOS; describe la ubicación de TREN·EXPRESO.
Para cada P en HITOS
R·SEÑAL·EN·P - con rango {-1,1}
E·SEÑAL·EN·P - con rango {-1,1}
Interacción entre componentes
La base temporal es discreta: t, t+1, t+2, ...
(a) El valor de R·SEÑAL·EN·P en el instante t es D((RAPIDO en t) - P) donde D(x) es 1 si x >= 0 y -1 si x < 0.
(b) El valor de E·SEÑAL·EN·P en el instante t es D((EXPRESO en t) - P).
(c) RAPIDO en t+1 = [RAPIDO en t] + [E·SEÑAL·EN·(RAPIDO en t) en t].
(d) EXPRESO en t+1 = [EXPRESO en t] + [R·SEÑAL·EN·(EXPRESO en t) en t].
El estado del modelo lo podemos representar por el par (r,e), como se muestra en la siguiente figura:
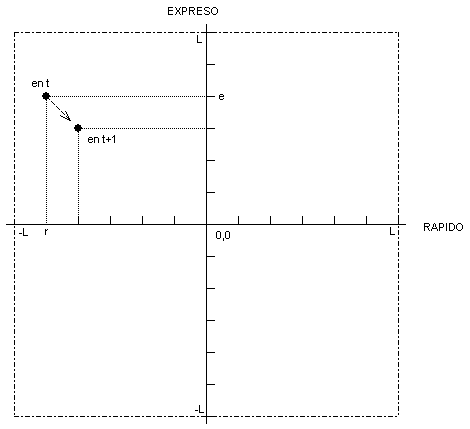 Verificamos ahora que RAPIDO y EXPRESO son variables de estado. Supongamos que conocemos los valores de RAPIDO y EXPRESO en el instante t. Llamemos a estos valores r y e, respectivamene. Veremos cómo calcular los valores de todas las variables descriptivas en t+1.
Verificamos ahora que RAPIDO y EXPRESO son variables de estado. Supongamos que conocemos los valores de RAPIDO y EXPRESO en el instante t. Llamemos a estos valores r y e, respectivamene. Veremos cómo calcular los valores de todas las variables descriptivas en t+1.
De (a), tenemos que para cada hito P: R·SEÑAL·EN·(P en t) = D(r-P)
Similarmente, E·SEÑAL·EN·(P en t) = D(e-P)
En particular, para el hito r (la ubicación del rápido):
R·SEÑAL·EN·(r en t) = D(r - r) = 1
E·SEÑAL·EN·(r en t) = D(e - r) (*)
Ejercicio: Calcular señales en el hito e en t.
De (c) y de (*) tenemos: RAPIDO en t+1 = r + E·SEÑAL·EN·(r en t) = r + D(e - r) (**)
Ejercicio: Calcule EXPRESO en t+1.
Usando (a) y (**) tenemos:
R·SEÑAL·EN·(P en t+1) = D((RAPIDO en t+1) - P) = D(r + D(e - r) - P)
(***)
Ejercicio: Calcular E·SEÑAL·EN·(P en t+1).
De las ecuaciones (**) y (***), y de los ejercicios, vemos que los valores de todas las variables descriptivas en t+1 se expresan en términos de r y e, los valores del rápido y el expreso en el instante t.
[anterior]
[home]
[siguiente]