[anterior]
[home]
[siguiente]
1.1. Modelamiento y simulación (introducción)
Entenderemos por "modelamiento y simulación" a las actividades asociadas con la
construcción de modelos de sistemas del mundo real, y su simulación en un
computador.
Los modelos son útiles para predecir y/o estudiar el comportamiento de un
sistema real, que puede servir para corroborar algunas hipótesis. Por ejemplo,
para predecir el movimiento de objetos en la superficie de la Tierra, sometidos
a la fuerza de gravedad, las ecuaciones de Newton son un modelo suficientemente
bueno. Con ellas se podría predecir cuál sería el movimiento (la posición
segundo a segundo) de un objeto que se suelta desde una altura determinada.
Sin embargo, si los objetos se mueven a velocidades comparables con la velocidad
de la luz, las ecuaciones de Einstein describen mejor su comportamiento.
Muchas veces se usan modelos de sistemas (que incluso puede que no existan
todavía) para ver cómo funcionan estos sistemas bajo distintas condiciones (con
distintos parámetros) y ver cuáles son las condiciones necesarias para que el
sistema sirva o trabaje en forma óptima. Hay muchas razones por las cuales es
conveniente experimentar en un modelo y no en la vida real: costos, tiempo,
peligro o simplemente imposibilidad. Los experimentos son repetibles. Algunos
ejemplos de sistemas de la vida real que pueden ser modelados son: supermercados,
hospitales, redes de caminos, represas, redes de computadores y modelos
económicos.
En general, los modelos son una simplificación de la vida real. Esto porque el
sistema real generalmente es muy complicado, o porque sólo se pretente estudiar
una parte del sistema real.
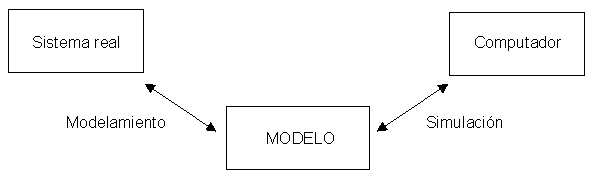
El proceso de definición del modelo de un sistema (real o no real) se llama
modelamiento. La simulación consiste en usar el modelo para generar
datos acerca del comportamiento del sistema para ver cómo se comportaría, bajo
el supuesto de que el modelo está bien hecho.
En general, cualquiera sea la forma que adopte, el modelo debe ser capaz de
proveer instrucciones a alguien o algo, de modo que pueda generar datos que
describan el comportamiento del sistema modelado. Así entonces, se tiene un
sistema real, cuyo modelamiento genera un modelo que puede
ser representado en un computador a través de una simulación.
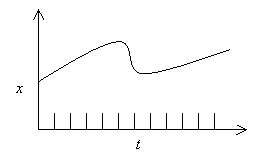
El "sistema real" es la parte del mundo real de nuestro interés. Como regla
general, podemos decir que el sistema real es una fuente de datos conductuales,
los cuales consisten en formas primarias de gráficos x versus t,
donde x puede ser cualquier variable de interés, tal como la
temperatura de un cuarto, el número de pétalos de una flor o el Producto Nacional
Bruto, y t es el tiempo, medido en unidades como segundos, días o años.
La siguiente figura muestra un ejemplo.
Un modelo es básicamente un conjunto de instrucciones para generar datos
conductuales (con cierto comportamiento) de la forma de la figura anterior. Los
modelos son algunas veces expresados en forma de ecuaciones diferenciales,
notación teórica de autómatas o en formalismo de eventos discretos.
¿Cómo se sabe si un modelo es bueno? Para saber si un modelo es bueno, basta
comparar los resultados que arroja con los del sistema real que se quiere
estudiar. La validez del modelo depende de "cuan bien el modelo representa al
sistema real" en términos de los datos arrojados por el modelo versus los datos
del sistema real. El problema es que muchas veces el sistema no existe, pues
puede ser un modelo de algo que se quiere construir. En todo caso, lo principal
de un modelo es que los resultados que arroje reflejen de alguna manera lo que se
quiere estudiar acerca del sistema que se está modelando.
No existe ninguna manera de saber cuál es el mejor modelo para un sistema. Es
posible comparar dos modelos y decidir cuál de ellos es mejor bajo algún punto
de vista particular, pero en ningún caso se puede saber exactamente cuándo se
está frente al mejor modelo para una situación dada.
[anterior]
[home]
[siguiente]


