Problema 1: Calcule el tiempo utilizado por el siguiente algoritmo:

int elevado(x,n){
    /* caso base */
    if (n == 0) {
        return 1;
    }
    /* caso recursivo impar*/
    else (n es impar) {
        return x * elevado(x,n-1);
    }
    /* caso recursivo par*/
    else (n es par) {
        return elevado(x*x,n/2);
    }
}

Solucion:

podemos ver que, si n es par:

f(n)	= 1+ f(n/2)

 

si n es impar:
 

f(n)	= 1 + f(n-1) = 1 + (1 + f ((n-1)/2)) = 2 + f((n-1)/2)

 

debido a esto, para cualquier n tenemos la cota:

desarrollando:

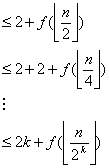
si n=2^k :

hemos mostrado entonces que f(n) es de orden O(log(n))

Otro enfoque:

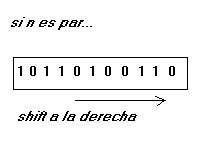
Un enfoque alternativo es pensar que cada vez que encontramos n par, el numero se reduce a la mitad. Expresando esto como en representación binaria, significa hacer un shift a la derecha en el número.

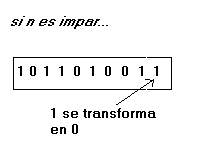
Por otra parte, cada vez que encontramos un n impar, el número se reduce en 1. lo que significa cambiar el ultimo digito bit de 1 a 0.

El total de operaciones por lo tanto, es el número de shifts realizados, más el número de 1's transformados a 0's. Como la representación binaria de n tiene log(n) digitos, tanto el número de shifts como el total de 1 transformados en 0 están acotados por log(n), lo que establece una cota de 2log(n) operaciones => f(n) es orden O(log(n)).
 
 
 

Problema 2: Calcule el tiempo utilizado por el siguiente algoritmo:

int sumaLista (lista l){
    if l.largo = 0
        return 0
    else l.largo = 1
        return l.primerElemento
    else sumaLista (l.mitadDerecha) + sumaLista (l.mitadIzquierda);
}

Supuestos:

• el cálculo de l.mitadDerecha y l.mitadIzquierda es de costo 1
• el cálculo de encontrar el primer elemento es de costo 1

f(1) = 1

Caso recursivo:
f(n) = 2*f(n/2) + 2
     = 2*(2*f(n/4) + 2) + 2 = 4*f(n/4) + 6 = 2²*f(n/2²) + 2*(2² - 1)
     = 4*(2*f(n/8) + 2) + 6 = 8*f(n/8) + 14 = 2³*f(n/2³) + 2*(2³ - 1)
     = ...
f(n) = 2^k*f(n/2^k) + 2*(2^k - 1)

suponiendo : n = 2^k => k = log₂n

f(n) = 2^k*f(1) + 2*(2^k - 1)
f(n) = n + 2*(n - 1)

f(n) = 3*n - 2 = O(n)

NOTA: este es otro ejemplo en donde la recursividad no sirve
 

Problema 3: Calcule el tiempo utilizado por el siguiente algoritmo

lista Msort(lista l){
    if (l.length < 2)
        return l;
    else{
        lDer= Msort(l.mitadDerecha);
        lIzq= Msort(l.mitadIzquierda) ;
        l= mezclaListas(lDer, lIzq);
        return l;
    }
}

Supuestos:

• la mezcla de elementos de la lista tiene costo tamaño de la lista
• el cálculo de l.mitadDerecha y l.mitadIzquierda es de costo 1.

T(1) = 1

No se considerarán las operaciones de costo unitario puesto que son de costo despreciable en la iteración (comparadas con el costo de redistribución en la lista)

Caso recursivo:
T(n) = 2*T(n/2) + n
     = 2*(2*T(n/4) + n/2) + n = 4*T(n/4) + n + n = 2²*f(n/2²) + 2*n
     = 4*(2*T(n/8) + n/4) + 2*n = 8*T(n/8) + n + 2*n = 2³*T(n/2³) + 3*n
     = ...
f(n) = 2^k*T(n/2^k) + k*n

suponiendo : n = 2^k => k = log₂n

f(n) = n*T(1) + n*log₂n
f(n) = n + n*log₂n = O(n*log₂n)

Problema 4: Resuelva la ecuación de la forma

T(n)= p*T(n/q) + K*n

Solución: desarrollemos

T(n)= K*n + p*T(n/q)
    = K*n + p(K*(n/q) + p*T(n/q²))
    = K*n * (1 + (p/q)) +  p²*T(n/q²)

(donde: T(n/q²)= K*(n/q²) + p*T(n/q³))

    = K*n * (1+(p/q)+(p/q)²) + p³*T(n/q³)

en general:

    = K*n * (1+(p/q)+(p/q)²+..+(p/q)^j-1) + p^j*T(n/q^j)

Los otros casos:

Caso p < q :

T(n) <= K*n *(1+(p/q)+(p/q)²+..) + n^(log_qn)

(donde: (1+(p/q)+(p/q)²+.. ) = 1/(1-(p/q)) )

=> = O(n)

Caso p = q :

T(n) = K*n *(1+1+1+..) + p^j*T(n/q^j)
            ^^^^^^^^
            j veces

j = log_qn =>

T(n) = K*n*log_qn + n*T(1)
     = O(n*log(n))