Auxiliar CC30A
Junio 15, 2001
Búsqueda en texto

Auxs: Bárbara Poblete, Rhodrigo Meza, Rodrigo Paredes

Búsqueda en texto: algoritmo Knuth-Morris-Pratt (KMP)

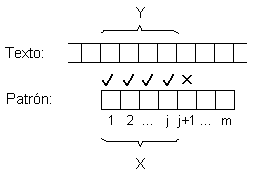
Suponga que se está comparando el patrón y el texto en una posición dada, cuando se encuentra una discrepancia.

La ventaja de KMP, es que permite avanzar varias posiciones a la vez, gracias a la función de fracaso:

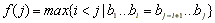
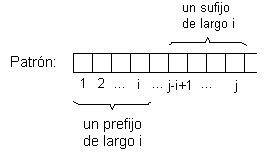
Intuitivamente, f(j) es el largo del mayor prefijo de X que además es sufijo de X. Note que j = 0 es un caso especial, puesto que si hay una discrepancia en b0 el patrón se desliza en una posición.

Si se detecta una discrepancia entre el patrón y el texto cuando se trata de calzar bj+1, se desliza el patrón de manera que bf(j) se encuentre donde bj se encontraba, y se intenta calzar nuevamente.

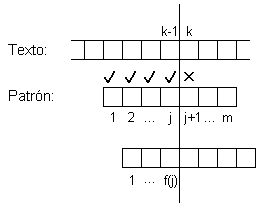
El algoritmo para generar la función de fracaso es el siguiente (es similar al algoritmo KMP): 

// m es largo del patron
// los indices comienzan desde 1
int[] f=new int[m];
f[1]=0;
int j=1;
int i;
while (j<m)
{
  i=f[j];
  while (i>0 && patron[i+1]!=patron[j+1])
  {
    i=f[i];
  }
  if (patron[i+1]==patron[j+1])
  {
    f[j+1]=i+1;
  }
  else
  {
    f[j+1]=0;
  }
  j++;
}
Ejemplo 1. analicemos el patrón aabaaa
 
Ejemplo de ejecución del patrón aabaaa
Comentarios
patrón (p[]) a a b a a a
fn. fracaso (f[]) 0 inicializaciones: f[1] = 0, j = 1, Intuitivamente: 0, 1, 0, 1, 2, 2
fn. fracaso (f[]) 0 1 i = f[j=1]= 0
i = 0 => no entra al while
p[i+1=1] == p[j+1=2] => f[j+1=2] = i+1 = 1
j = 2
fn. fracaso (f[]) 0 1 0 i = f[j=2]= 1
i = 1 => entra al while, p[i+1=2] != p[j+1=3] => i = f[i=1] = 0, sale del while
p[i+1=1] != p[j+1=3] => f[j+1=3] = 0
j = 3
fn. fracaso (f[]) 0 1 0 1 i = f[j=3]= 0
i = 0 => no entra al while
p[i+1=1] == p[j+1=4] => f[j+1=4] = i + 1 = 1
j = 4
fn. fracaso (f[]) 0 1 0 1 2 i = f[j=4]= 1
(i = 1) && (p[i+1=2] == p[j+1=5] ) =>  no entra al while
p[i+1=2] == p[j+1=5] => f[j+1=5] = i + 1 = 2
j = 5
fn. fracaso (f[]) 0 1 0 1 2 2 i = f[j=5]= 2
i = 2 => entra al while, p[i+1=3] != p[j+1=6] => i = f[i=2] = 1,
                                   p[i+1=2] == p[j+1=6], sale del while
p[i+1=2] == p[j+1=6] => f[j+1=6] = i + 1 = 2
j = 6, sale while principal

Ejemplo 2. analicemos el patrón ababac
 

Ejemplo de ejecución del patrón aaaab
Comentarios
patrón (p[]) a b a b a c
fn. fracaso (f[]) 0 inicializaciones: f[1] = 0, j = 1, Intuitivamente: 0, 0, 1, 2, 3, 0
fn. fracaso (f[]) 0 0 i = f[j=1]= 0
i = 0 => no entra al while
p[i+1=1] != p[j+1=2] => f[j+1=2] = 0
j = 2
fn. fracaso (f[]) 0 0 1 i = f[j=2]= 0
i = 0 => no entra al while
p[i+1=1] == p[j+1=3] => f[j+1=3] = i+1= 1
j = 3
fn. fracaso (f[]) 0 0 1 2 i = f[j=3]= 1
(i = 1) && (p[i+1=2] == p[j+1=4] ) => no entra al while
p[i+1=2] == p[j+1=4] => f[j+1=4] = i + 1 = 2
j = 4
fn. fracaso (f[]) 0 0 1 2 3 i = f[j=4]= 2
(i = 1) && (p[i+1=3] == p[j+1=5] ) =>  no entra al while
p[i+1=3] == p[j+1=5] => f[j+1=5] = i + 1 = 3
j = 5
fn. fracaso (f[]) 0 0 1 2 3 0 i = f[j=5]= 3
i = 3 => entra al while, p[i+1=4] != p[j+1=6] => i = f[i=3] = 1,
                                   p[i+1=2] != p[j+1=6] => i = f[i=1] = 0, sale del while
p[i+1=1] != p[j+1=6] => f[j+1=6] = 0
j = 6, sale while principal

Búscando casos malos:

Supongamos que el texto esta compuesto por 10 letras a:

aaaaaaaaaa

Y que nuestro patrón es aaaab. Claramente este es un peor caso para fuerza bruta, gasta O(n*m) para decir que falló

la función de fracaso KMP es:
 

Función de fracaso del patrón aaaab
patrón (p[]) a a a a b
función de fracaso (f[]) 0 1 2 3 0

KMP realiza la siguiente ejecución:

aaaab
12345

aaaaaaaaaa
1234
   34
    34
     34
      34
       34
        34

KMP gasta O(n+m) para decir que falló!!

Búsqueda en texto: algoritmo Boyer-Moore-Horspool (BMH)

Los algoritmos Fuerza Bruta y Knuth-Morris-Pratt (KMP) tratan de calzar el patrón buscado en el texto de izquierda a derecha, como se muestra en la siguiente figura:

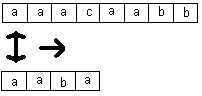
Boyer y Moore sugirieron un método alternativo: buscar dentro del patrón de derecha a izquierda, mientras el patrón completo se mueve en el texto de izquierda a derecha, tal como se muestra en la siguiente figura:

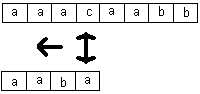
Horspool realizó algunas simplificaciones al algoritmo original, resultando el algoritmo conocido como BMH. La idea de BMH es:

Sea P[1..m] el patrón de busqueda, que contiene m caracteres. Para saber cuanto hay que avanzar en caso de encontrar una discrepancia, es necesario construir antes de realizar la búsqueda en el texto una tabla que indique cuántos caracteres avanzar en cada caso. Se denominará a la tabla siguiente(s) y se define como:

siguiente(s):

Ejemplo de BMH: 
Texto: analisis de algoritmos
Patrón: algo

Tabla siguiente:  g->3
                  l->2
                  a->1

        analisis de algoritmos
        algo
          algo
              algo
                  algo
                    algo
Eficiencia del algoritmo: En promedio, si m es el largo del patrón, n el largo del texto y c el tamaño del alfabeto, el número esperado de comparaciones es n(1/m+1/2c).

Ejemplo 3. Calculemos la tabla siguiente del patrón abracadabra
 
Tabla siguiente patrón abracadabra
a
b
c
d
e
f
g
h
i
j
k
l
m
n
ñ
o
p
q
r
s
t
u
v
w
x
y
z
8
9
5
7
0
0
0
0
0
0
0
0
0
0
0
0
0
0
10
0
0
0
0
0
0
0
0

Ejemplo 4. Calculemos la tabla siguiente del patrón australopitecus
 
Tabla siguiente patrón australopitecus
a
b
c
d
e
f
g
h
i
j
k
l
m
n
ñ
o
p
q
r
s
t
u
v
w
x
y
z
6
0
13
0
12
0
0
0
10
0
0
7
0
0
0
8
9
0
5
3
11
14
0
0
0
0
0

Otro ejemplo de BMH:

Texto:  se hacen armarios a pedido
Patrón: armar
 
Tabla siguiente patrón armar
a
b
c
d
e
f
g
h
i
j
k
l
m
n
ñ
o
p
q
r
s
t
u
v
w
x
y
z
4
0
0
0
0
0
0
0
0
0
0
0
3
0
0
0
0
0
2
0
0
0
0
0
0
0
0

se hacen armarios a pedido
armar                    , en el texto hay una a, luego la alineamos con la última a del patrón
 armar                   , en el texto hay una c, saltamos el patrón completo
      armar              , en el texto hay una r, luego la alineamos con la última r del patrón, sin contar la última letra
         armar           , patrón encontrado!!

Búscando casos malos:

Supongamos que el texto esta compuesto por 10 letras a:

aaaaaaaaaa

Y que nuestro patrón es baaaa. En este caso la fuerza bruta, gasta O(n) para decir que falló

la tabla siguiente BMH es:
 

Tabla siguiente patron aaaab
a
b
4
1

BMH realiza la siguiente ejecución:

aaaaaaaaaa
baaaa
 baaaa
  baaaa
   baaaa
    baaaa
     baaaa

Este es un peor caso para BMH  O(m*n)!!

Búsqueda multipatrón en un texto

Cuando se desea buscar múltiples patrones en un texto utilizando el algoritmo BMH, se procede de la siguiente forma:

Texto: se venden armarios a pedido
Patrónes: arma, rios

Tabla siguiente arma:
a->1, r->2, m->3, todas las demas son 0

Tabla siguiente rios:
r->1, i->2, o->3, todas las demas son 0

se venden armarios a pedido
arma
rios                      , fallan los dos patrones y en ninguno hay v => salto completo
    arma
    rios                  , fallan los dos patrones y en ninguno hay e => salto completo
        arma
        rios              , fallan ambos, pero ambos tiene la r, luego el salto menor es el que alinea la r de arma
          arma
          rios            , patrón arma encontrado!!