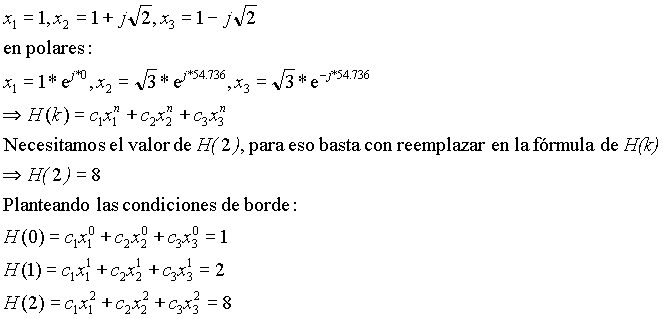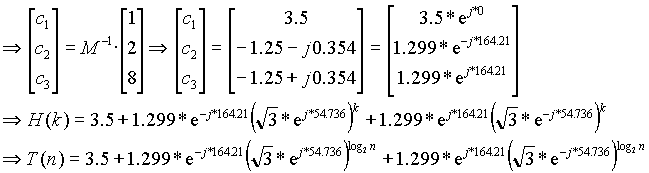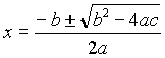
Clase Auxiliar 08/09/2000
Problema 1: Calcule el tiempo utilizado por el siguiente algoritmo:
int elevado(x,n){
/* caso base */
if (n == 0) {
return 1;
}
/* caso recursivo impar*/
else (n es impar) {
return x * elevado(x,n-1);
}
/* caso recursivo par*/
else (n es par) {
return elevado(x*x,n/2);
}
}
Con esta información:
f(1) = 1
Caso impar:
f(n) = f(n-1) + 1
= (f(n-2) + 1) + 1
= f(n-2) + 2
= ...
= f(1) + n - 1
= 1 + n - 1
f(n) = n
Caso par:
f(n) = f(n/2) + 1 = f(n/21) + 1
= (f(n/4) + 1) + 1 = f(n/4) + 2 = f(n/22)
+ 2
= (f(n/8) + 1) + 2 = f(n/8) + 3 = f(n/23)
+ 3
= ...
= f(n/2k) + k
suponiendo: n = 2k => k = log2n
f(n) = f(2k/2k) + k = f(1) + k = 1 + k
f(n) = 1 + k = 1 + log2n
f(n) = 1 + log2n
La pregunta es ¿cuántas veces se repite el caso impar?
Respuesta la misma cantidad de veces que se repite el caso par
luego el n en el caso impar es en realidad log2n por lo que el resultado final considerando los casos pares e impares es:
f(n) = 2 + 2*log2n = O(log2n)
Problema 2: Calcule el tiempo utilizado por el siguiente algoritmo:
int sumaLista (lista l){
if l.largo = 0
return 0
else l.largo = 1
return l.primerElemento
else sumaLista (l.mitadDerecha) + sumaLista
(l.mitadIzquierda);
}
Supuestos:
f(0) = 1
f(1) = 1
Caso recursivo:
f(n) = 2*f(n/2) + 1
= 2*(2*f(n/4) + 1) + 1 = 4*f(n/4) + 3
= 22*f(n/22) + 22 - 1
= 4*(2*f(n/8) + 1) + 3 = 8*f(n/8) + 7
= 23*f(n/23) + 23 - 1
= ...
f(n) = 2k*f(n/2k) + 2k - 1
suponiendo : n = 2k => k = log2n
f(n) = 2k*f(1) + 2k - 1
f(n) = n + n - 1
f(n) = 2*n - 1 = O(n)
NOTA: este es otro ejemplo en donde la recursividad no sirve
Problema 3: Calcule el tiempo utilizado por el siguiente algoritmo:
lista Qsort(lista l){
if l.length < 2
return l
else{
pivote = l.elemDelMedio
redistribuir los elementos
de l de modo que los menores queden a la derecha del pivote y los mayores
a la izquierda
lDer= Qsort(l.derechaPivote);
lIzq= Qsort(l.izquierdaPivote);
return lDer.concatena(lIzq);
}
}
Supuestos:
T(1) = 1
No se considerarán las operaciones de costo unitario puesto que son de costo despreciable en la iteración (comparadas con el costo de redistribución en la lista)
Caso recursivo:
T(n) = 2*T(n/2) + n
= 2*(2*T(n/4) + n/2) + n = 4*T(n/4) +
n + n = 22*f(n/22) + 2*n
= 4*(2*T(n/8) + n/4) + 2*n = 8*T(n/8)
+ n + 2*n = 23*T(n/23) + 3*n
= ...
f(n) = 2k*T(n/2k) + k*n
suponiendo : n = 2k => k = log2n
f(n) = n*T(1) + n*log2n
f(n) = n + n*log2n = O(n*log2n)
Problema 4: Resuelva la ecuación de recurrencia fn = 3fn-1 - 2fn-2 mediante:
f0 = 0
f1 = 1
a. Planteando el polinomio característico
b. Adivinando la serie, y demostrando su validez
a. Polinomio característico
fn - 3fn-1 + 2fn-2 = 0
Suponiendo solución exponencial (fn ~ xn)
xn - 3xn-1 + 2xn-2 = 0 / · x2-n
x2 - 3x + 2 = 0
resolviendo el polinomio cuadrático
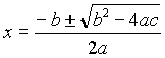
=> x1 = 2, x2 = 1
Proponiendo la solución de la forma:
fn = C1x1n + C2x2n
Con esta información, ya se puede decir que la solución
es O(2n).
Hay que encontrar el valor de las constantes C1 y
C2
f0 = C1x10 + C2x20
= 0
f1 = C1x11 + C2x21
= 1
Evaluando:
f0 = C1 + C2 = 0
f1 = 2C1 + C2 = 1
Resolviendo el sistema matricial de 2 x 2
C1 = 1, C2 = -1
=> fn = C1x1n - C2x2n = 1*2n - 1*1n = 2n - 1
=> fn = 2n - 1 = O(2n)
b) Adivinando la serie, y demostrándola
f0 = 0
f1 = 1
f2 = 3
f3 = 7
=> fn = 2n - 1
Lo interesante es demostrar esto :)
Dado:
fn = 2n - 1
fn-1 = 2n-1 - 1
Demostrar que: fn+1 = 2n+1 - 1
fn+1 = 3fn - 2fn-1
fn+1 = 3*(2n - 1) - 2(2n-1 - 1)
fn+1 = 3*2n - 3 - 2*2n-1 + 2
fn+1 = 3*2n - 2n -1
fn+1 = 2*2n -1
=> fn+1 = 2n+1 -1, con lo que se obtiene que fn = O(2n)
QED (queda esto demostrado)
Problema 5: Resuelva la ecuación de recurrencia fn = fn-1 - fn-2 planteando su polinomio característico.
f0 = 0
f1 = 1
fn - fn-1 + fn-2 = 0
Suponiendo solución exponencial (fn ~ xn)
xn - xn-1 + xn-2 = 0 / · x2-n
x2 - x + 1 = 0
resolviendo el polinomio cuadrático
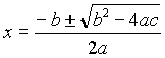
=> 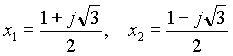
en coordenadas polares:
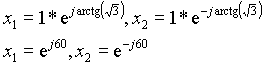
Proponiendo la solución de la forma:
fn = C1x1n + C2x2n
Con esta información, ya se puede decir que la solución
es O(1), en realidad gira torno al circulo unitario.
Hay que encontrar el valor de las constantes C1 y
C2
f0 = C1x10 + C2x20
= 0
f1 = C1x11 + C2x21
= 1
Evaluando:
f0 = C1
+ C2 = 0
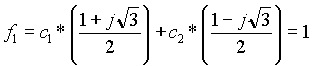
Resolviendo el sistema matricial de 2 x 2
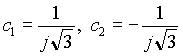
=> fn = C1x1n - C2x2n
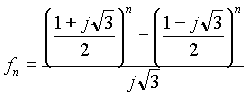
en coordenadas polares:
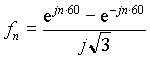
utilizando ejt = cos(t) + j*sen(t):
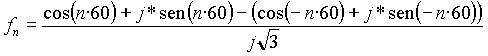
recordando que coseno es función par, seno es función impar y reduciendo los términos:
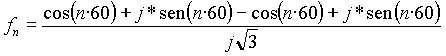

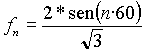
Notar que a pesar de que pasamos por números complejos, y que
se usaron funciones trigonométricas, los resultados de la serie
son todos enteros !!
Problema 6: Resuelva la ecuación de recurrencia T(n) = 2T(n/2) - 3T(n/4) + 7
T(1) = 1
T(2) = 2
Hint: realice un cambio de variables, elimine el término constante y resuelva el polinomio característico.
Cambio de variables: n = 2k, luego H(k) = T(2k) = T(n)
también cambian las condiciones de inicio:
H(0) = 1
H(1) = 2
Con esto tenemos:
(1) H(k) = 2H(k-1) - 3H(k-2) + 7
Para eliminar el término constante, consideremos H(n-1)
(2) H(k-1) = 2H(k-2) - 3H(k-3) + 7
Calculando (1) - (2)
H(k) - 3H(k-1) + 5H(k-2) - 3H(k-3) = 0
Suponiendo solución exponencial (H(k) ~ xn)
xk - 3xk-1 + 5xk-2 - 3xk-3
= 0 / · x3-k
x3 - 3x2 + 5x - 3 = 0
las raíces del polinomio son: