Un algoritmo simple para calcular xn es la siguiente:
y = 1;
for(j=n; j > 0; j--)
{
y = y*x;
}
El invariante de este algoritmo se puede escribir como y*xj
== xn, y el tiempo que demora el algoritmo es O(n). Implemente
un algoritmo que realice el cálculo de manera más eficiente,
es decir, que su complejidad temporal sea menor que O(n).
Solución:
Para encontrar un algortimo más eficiente hay que desligar las dos x's del invariante de la siguiente manera:
y = 1;
z = x;
for(j=n; j>0; j--)
{
y = y * z;
}
En este caso, el invariante se puede escribir como: y*zj
== xn.
¿Para que sirve esto? Esto nos permite modificar z si lo hacemos sin modificar el invariante. En particular, si j es par, podemos hacer:
z = z*z; j = j/2;El invariante no cambia, pero ahora j disminuye mucho más rápido. Más aún, si j sigue siendo par, se puede repetir lo anterior tantas veces como sea posible. El algoritmo queda como sigue:
y = 1;
z = x;
for(j=n; j>0; j--)
{
while(j es par)
{
z = z*z;
j = j/2;
}
y = y*z;
}
La complejidad temporal del nuevo algoritmo es O(log(n)).
Problema 2: Diagramas de estado
Escriba un algoritmo que cuente las palabras de una frase, y dibuje el diagrama de estados respectivo. Para simplificar suponga que la frase se encuentra en un string s, por ejemplo:
String s = "Hoy no se fia mañana si.";Una palabra se define como una secuencia de caracteres consecutivos distintos de ' ' (espacio en blanco). Suponga que las frases terminan en '.' (punto).
Solución:
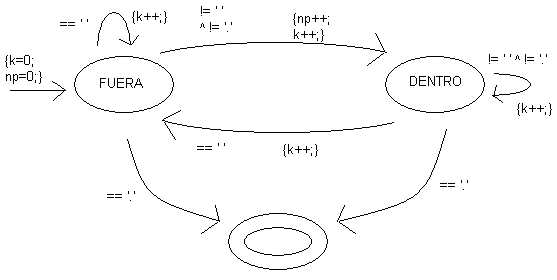
Se examinan los caracteres de izquierda a derecha, y el proceso depende si se está dentro o fuera de una palabra.
El diagrama de estados del algoritmo es:

Primera versión del algoritmo:
np = 0;
estado = FUERA;
k=0;
c = s.charAt(k);
for(k=1; c != '.'; k++)
{
if(estado == FUERA)
{
if(c != ' ')
{
np++;
estado = DENTRO;
}
}
else
{
if(c == ' ')
{
estado = FUERA;
}
}
c = s.charAt(k);
}
Segunda versión del algoritmo:
k = 0;
np = 0;
while(s.charAt(k) != '.')
{
// estado == FUERA
while(s.charAt(k) == ' ')
{
k++;
}
if(s.charAt(k) == '.')
{
break;
}
np++;
k++;
// estado == DENTRO
while(s.charAt(k) != ' ' && s.charAt(k) != '.')
{
k++;
}
}
Problema 3: Más diagramas de estado
Suponga que existe un arreglo a con n casilleros, en donde se almacenan números enteros. Escriba un algoritmo, y su correspondiente diagrama de estados, que reordene los elementos del arreglo dejando a la izquierda los números menores que 0 y a la derecha los números mayores o iguales a 0.
Solución:
El diagrama de estados del algoritmo es:
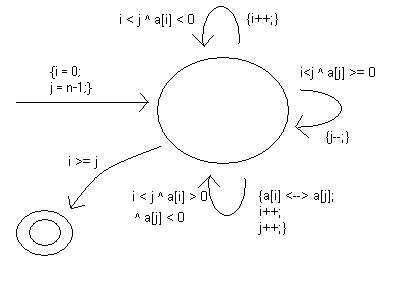
i = 0;
j = n-1; //ultima posicion de arreglo de n elementos tiene indice (n-1)
while(i < j)
{
if(a[i] < 0)
{
i++;
}
else if(a[j] >= 0)
{
j--;
}
else
{
a[i] <--> a[j]; //swap entre a[i] y a[j]
i++;
j--;
}
}
Segunda versión del algoritmo:
i = 0;
j = n-1; //ultima posicion de arreglo de n elementos tiene indice (n-1)
while(i < j)
{
while(i < j && a[i] < 0)
{
i++;
}
while(i < j && a[j] >= 0)
{
j--;
}
if(i < j)
{
a[i] <--> a[j];
i++;
j--;
}
}
Solución alternativa:
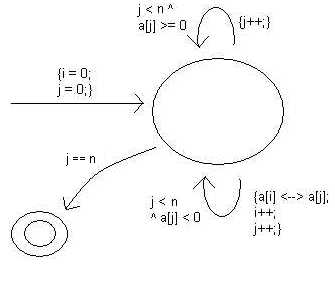
i = 0;
for(j = 0; j < n; j++)
{
if(a[j] < 0)
{
a[i] <--> a[j];
i++;
}
}