A simple “How To” for Maple

Contents

• 1  Introduction
• 2  How to...
  • 2.1  Evaluate an expression numerically?
  • 2.2  Plot a single variable function?
  • 2.3  Plot two variables functions?
  • 2.4  Solve an equation?
  • 2.5  Solve a system of equations?
  • 2.6  Compute the derivative of a function?
  • 2.7  Compute primitives, integrals?
  • 2.8  Make substitutions?

1  Introduction

This article is a list of small useful tricks for Maple, like “How to plot a two variable function?”, “How to evaluate an expression numerically?” and so on... Every item is self-contained and only simple examples are provided with a brief comment so you can save your time! The examples were tested under Maple 10.

2  How to...

2.1  Evaluate an expression numerically?

> eval(2^(1/2)); 1.414213562

2.2  Plot a single variable function?

First set the function, or the expression that define the function:

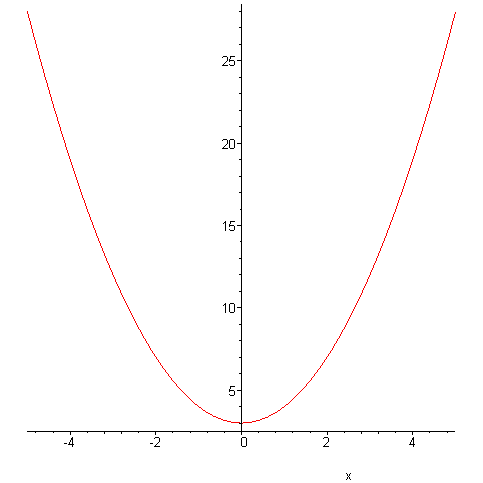
> f:= x^2 + log(x);

Then use the plot command:

> plot(f,x=-1..10);

Which gives:

 
 > f1:= x^2 + 3;
 > f2:= 2*x+3;
 > plot(f1,f2,x=-10..10);
 	
		

2.3  Plot two variables functions?

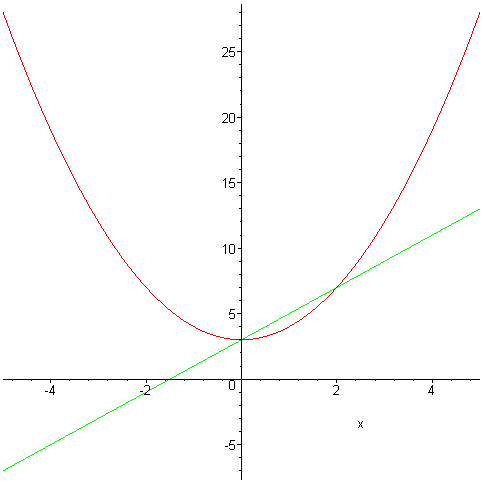
First define the function, for example:

> f:= x^2 - y^3;

Then use the plot3d command:

plot3d(f,x=-5..5,y=-2..2,grid=[10,10],axes=normal);

The parameter grid defines the frequency of plotting. We get:

2.4  Solve an equation?

> solve(x^2-4=0,x); 2, -2

2.5  Solve a system of equations?

> solve({x-4* y =0,y + x + 3=0},{x,y}); {x = -12/5, y = -3/5}

2.6  Compute the derivative of a function?

Define the function:

> f:= x^2+3+y;

Then use the command diff with the expression of the function and the variable of derivation.

> diff(f,x); 2*x > diff(f,y); 1

You can derivate many times like that:

> diff(x^4, x$2); 12*x^2

2.7  Compute primitives, integrals?

For obtaining the primitive of  f(x)=x²:

> int(x^2,x); 1/3*x^3

Integrating  f(x)=x² on the interval [1,3]:

> int(x^2,x=1..3); 26/3

2.8  Make substitutions?

> subs({x=10,t=1,a=3},x+a+t+w); 14 + w

This document was translated from L^AT_EX by H^EV^EA.