4.1.1 Clasificadores

4.1.1.1 Inductor de Árboles de Decisión

El algoritmo para inducir un árbol de decisiones es el conocido ID3 [20]. Lo que se pretende con el algoritmo, es llegar a un árbol que describe a los datos entrantes. Como ejemplo se muestra el siguiente árbol de decisión:

A partir de uno de estos gráficos, es muy sencillo ver las reglas asociadas, como por ejemplo:

•  
• Sí el clima es soleado, y la humedad es baja, entonces se puede jugar tenis

   

• Si el clima es lluvioso, y el viento es fuerte, entonces no se puede jugar tenis.

En términos algebraicos esto sería

SOLEADO Ù ØHUMEDO Þ SÍ

LLUVIOSOÙ (VIENTO = BAJO) Þ NO

El problema principal es como se puede llegar de un conjunto de datos, a un árbol de decisión. El árbol en la ilustración 10 es obtenido desde la tabla siguiente

El algoritmo para producir un árbol de esta naturaleza es:

Dado los atributos A_i y un conjunto de Datos D

•  
• Elegir un atributo – asignarlo como el atributo de decisión para nodo

   

   

• ---

  Para cada valor de A, se crea un nuevo descendiente, o hijo

   

• Se ordenan los Datos con respecto a los valores de los hijos de A

   

   

• ---

  Si se clasifica perfectamente a los datos, entonces se para. Si no se llega a una clasificación perfecta, entonces se vuelve a iterar con los hijos

El problema con este algoritmo, es que se llega a un árbol bastante grande, y quizás con muchas clasificaciones redundantes. Unas maneras de mejorar el algoritmo sería mediante:

•  
• Podadas del árbol, de abajo hacia arriba, para eliminar ramas redundantes

   

• Elegir las ramas más pequeñas, dado que generalmente estas son las más útiles y las que mejor describen a la realidad[10]

Dado que los arboles de decisión son utilizados para la clasificación de información, son mas aptos para los siguiente escenarios:

•  
• Instancias son descritas por un conjunto finito de pares atributo-valor

   

• La información, en general, puede ser discretizado en intervalos disjuntos

   

• Cuando se requieren expresiones disjuntas de la información

   

• Cuando la información contiene mucho ruido

4.1.1.1.1 Problemas con los Árboles de Decisión

Existen varios problemas asociado a la creación de los árboles de decisión. Generalmente, como se evidencio anteriormente se puede llegar al sobre-calce, o "overfitting" , de la información. Esto implica que el árbol resultante será de tamaño enorme, y con muchas hipótesis redundantes.

Existe un conjunto de heurísticas que permite evitar el overfitting. Tales incluyen a:

•  
• No hacer que el árbol calce con todos los ejemplos, parando su crecimiento antes de llegar al final del conjunto de entrenamiento.

   

• Hacer calzar el árbol con todos los ejemplos, y posteriormente podar.

El overfitting no es un problema hasta que es identificado como tal. Para ver si el árbol está sobre entrenado, existen algunas medidas que se pueden efectuar, una vez que el árbol esta listo.

•  
• Usar un conjunto de prueba que se aplica al árbol, una vez completado, para verificar la existencia de overfitting.

   

• Usar pruebas estadísticas para comprobar si cambios en el árbol mejoran resultados obtenidos con conjunto de prueba (Ej. La Métrica, Chi-Cuadrado).

4.1.1.1.2 Parámetros asociado a ID3

El ID3 se basa, en que el conocimiento reduce incertidumbre, y por lo tanto entrega información. Este concepto se asociará con el termino entropía. Mientras más información se tiene, menos entropía existe, por lo que definiremos a

El valor de la entropía se puede calcular mediante la siguiente función

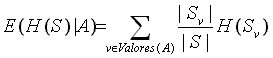
Donde

Es la Entropía de la Fuente Original S

Es un atributo que puede tomar Valores(A), valores distintos

Es un subconjunto de S, donde A = v

Es la Entropía de

Por lo que podemos definir la ganancia obtenida, de saber el valor de A, mediante la siguiente función

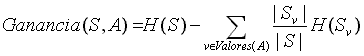
Cuyo valor corresponde al espacio recuperado por el conocimiento de A.

4.1.1.1.2 Seudo Código del Algoritmo ID3

4.1.1.2 Algoritmo de Naive Bayes

El fundamento detrás de este algoritmo es el teorema de Bayes.

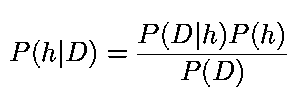
D : Datos de Entrenamiento

h : Hipótesis

El teorema se utiliza para encontrar la hipótesis más probable dado la información de entrenamiento. Para esto, se elige la probabilidad más alta mediante la maximización de la función. Reduciendo Max P(h/D) se llega a:

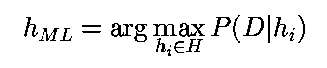
Suponiendo que P(h_i)=P(h_j)

Naive Bayes hace el supuesto de que existe independencia condicional entre los atributos:

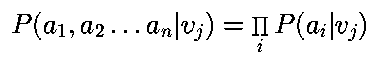
Por lo que se tiene que el clasificador de Naive Bayes es:

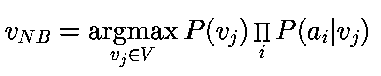
El algoritmo de aprendizaje de Naive Bayes sería entonces:

Aprendizaje_Naive_Bayes(Ejemplos)

{

Para Cada Valor v_j

Estimar P(v_j)

Para cada valor de atributo a_i

Estimar P(a_i/v_j)

}

Clasificar_nuvea_instancia(x)

V_NB = arg MAX P(v_j) Õ P(a_i/v_j)

v_jeV a_iex

 

 

Copyright Nelson Flores 2001™.

Departamento de Ciencias de la Computacion, Universidad de Chile.