[anterior]
[home]
[siguiente]
3.4. Recorrido de árboles
Suponga un árbol T con raiz ro. Queremos visitar (recorrer) cada nodo una vez. Hay varias maneras de hacerlo.
Recorrido desde abajo ("bottom-up"). Comenzando en la raiz, visite cada nodo sólo después de haber visitado a todos sus hijos (de izquierda a derecha). Ejemplo:
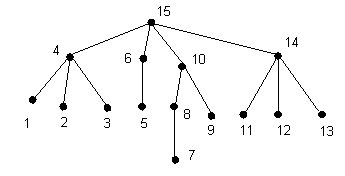
Recorrido desde arriba ("top-down"). Comenzando con la raiz, visite cada nodo antes de visitar a cualquier hijo. Continúe con los hijos antes de visitar un hermano. Ejemplo:
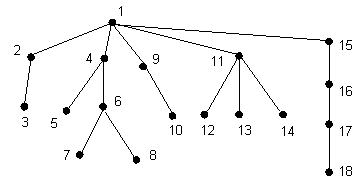
Funciones relacionadas con pesos
Para cada problema de centralidad que se desee resolver deben existir dos funciones llamadas COMBINE y EXTRACT, tales que:
e(v) = EXTRACT( v, WTS(v))
wt(u, v) = COMBINE(u, v, OTHER_WTS(v, u))
Observemos que cuando v es una hoja, OTHER_WTS(v, u) está vacío. Así, es posible ir calculando los pesos wt(u, v) "subiendo" en el árbol, es decir, con un recorrido desde abajo.
El algoritmo que estudiaremos hace dos recorridos del árbol. En el primero, desde abajo, calcula wt(padre(v), v). En el segundo, desde arriba, calcula wt(v, padre(v)) y las excentricidades.
Para calcular los pesos wt(padre(v), v), necesitamos una cantidad que resuma los aportes de todas las ramas incidentes a v. Esta cantidad la llamaremos SMR(v). El peso wt(padre(v), v) será entonces SMR(v), agregando información sobre el vértice v y extrayendo el peso de la rama(v, padre(v)).
Por ejemplo, en el problema 3:
wt(w, v) = å x Î V(w, v) c(x) Entonces:
SMR(v) = å x Î Ady(v) wt(v, x)
wt(w, v) = SMR(v) - wt(v, w) + c(v)
Finalmente, la opción COMBINE vamos a descomponerla en dos funciones: MAKESUM y SUBTRACT (en el caso general), para el segundo recorrido:
SMR(v) = MAKESUM(v, WTS(v))
wt(w, v) = SUBTRACT(v, w, SMR(v), wt(v, w))
Con esto, podemos presentar el algoritmo Rosenthal-Pino.
Algoritmo de Rosenthal-Pino
Input: Un árbol con raiz.
Output: Excentricidades para todos los vértices.
Método: Dos recorridos sobre el árbol. Utiliza funiones COMBINE, EXTRACT, MAKESUM, SUBTRACT (dependientes del problema).
1. v ¬ primer vértice de recorrido desde abajo
2. WHILE v ¹ ro
BEGIN
3. wt(padre(v), v) ¬ COMBINE(padre(v), v, OTHER_WTS(v, padre(v))); /* note que lo que está en OTHER_WST( ) se calculó cuando se procesó Hijos(v) */
4. v ¬ sucesor(v) en recorrido desde abajo;
END;
5. v ¬ ro; /* segundo recorrido */
6. e(ro) ¬ EXTRACT(ro, WTS(ro)); /* lo en WTS(ro) ya calculado */
REPEAT
7. SMR(v) ¬ MAKESUM(v, WTS(v));
8. FOR cada hijo w de v :
BEGIN
9. wt(w, v) ¬ SUBTRACT(v, w, SMR(v), wt(v, w));
10. e(w) ¬ EXTRACT(w, WTS(w));
END
11. v ¬ sucesor(v) en recorrido desde arriba; /* exceptuando hojas */
UNTIL se visitan todos los vértices no hojas
END;
Veamos ahora cómo podemos aplicar este algoritmo a los tres problemas que planteamos.
Problema 1. (centro)
Como entrada están los largos de cada arco l(u, v). El peso de una rama L(padre(v), v) es la distancia máxima de padre(v) a cualquier vértice z en la rama. Pero la trayectoria de padre(v) a z debe tener a v como el primer vértice después de padre(v). Así:
3. wt(padre(v), v) ¬ max(OTHER_WTS(v, padre(v))) + l(padre(v), v)
El resumen SMR deun vértice v es un vector de dos componentes. SMR1 es la distancia máxima desde v a cualquier punto en el árbol (¡así que también es la excentricidad de v!). Si u es el primer vértice en una trayectoria de v a un vértice en el cual se logra SMR1(v), entonces SMR2(v) es la distancia más larga de v a cualquier punto donde la trayectoria no pasa por u.
Elija u tal que wt(v, w) = SMR1(v). (cualquier u que cumpla esto es aceptable, si hay más de uno). Entonces:
SMR2(f(v)) ¬ max(OTHER_WTS(v, w))
y así:
9. wt(w, v) ¬ { SMR1(v) + l(w, v) si wt(v, w) ¹ SMR1(v), o SMR2(v) + l(w, v) en caso contrario }
10. e(w) ¬ SMR1(w)
Problema 2 (red con pérdidas)
Las entradas son las demandas c: V ® R y las funciones de los arcos g(u, v): R ® R.
El peso de una rama L(padre(v), v) es el número de unidades de energía que se necesitan en padre(v) para proveer los vértices de la rama.
3. wt(padre(v), v) ¬ g(padre(v), v)(total(OTHER_WTS(padre(v), v)) + c(v))
El resumen SMR de un vértice es la energía total que necesita para proveer los vértices que van desde v (no incluyéndolo):
SMR(v) ¬ total(WTS(v))
9. wt(w, v) ¬ g(w, v)(SMR(v) - wt(v, w) + c(v))
10. e(w) ¬ total(WTS(w))
Problema 3 (centroide)
Las entradas son las demandas en los vértices c: V ® R. El peso de una rama es la demanda total de los vértices de la rama:
3. wt(padre(v), v) ¬ total(OTHER_WTS(v, padre(v))) + c(v)
El resumen SMR de un vértice v esla demanda total del árbol desde vértices distintos de v.
SMR(v) ¬ total(WTS(v))
9. wt(w, v) ¬ SMR(v) - wt(v, w) + c(v)
10. e(w) ¬ max(WTS(w))
[anterior]
[home]
[siguiente]


