Luis Guerrero - Curso CC20A - Modelamiento de redes (cont.2)

3.3. Centralidad en árboles

En un grafo, en general G(V, X):

Definición. La distancia d(u, v) entre dos puntos u, v Î V es el largo de la trayectoria más corta que los une, si es que la hay; en caso contrario, d(u, v) = ¥.

Definición. La excentricidad e(v) de un punto v en un grafo conexo G es max d(u, v), para todo u en G. El radio r(G) es la excentricidad mínima de los puntos. Un punto v es un punto central si e(v) = r(G), y el centro de G es el conjunto de todos los puntos centrales.

Ejemplo. Excentricidades de cada punto.

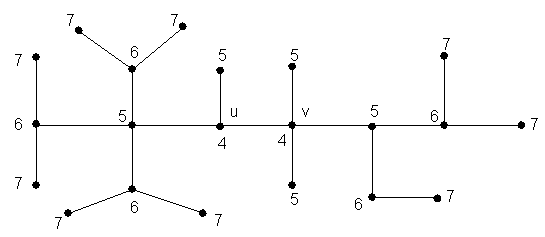
En este ejemplo, el radio es 4 y el centro consiste de dos puntos, u y v, cada uno con excentricidad mínima 4.

Teorema. Cada árbol tiene un centro consistente de uno o dos puntos adyacentes.

Definición. Una rama en un punto u de un árbol T es un subárbol maximal que contiene u como un vértice final ("hoja"). Así, el número de ramas en u es grad u.

Definición. El peso en un punto u de T (T árbol) es el número máximo de líneas en cualquier rama de u.

Los pesos en los puntos no-hojas se muestran en este ejemplo:

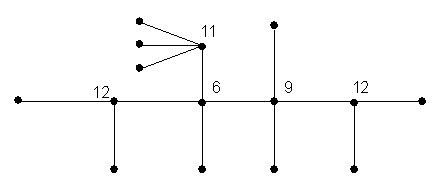
¿Cuánto es el peso en las hojas?

Definición. Un punto v es un punto centroide de un árbol T si v tiene mínimo peso, y el centroide de T consiste de todos estos puntos.

Teorema. Todo árbol tiene un centroide que consiste de uno o dos puntos adyacentes.

La definición de centro y centroide nos permite modelar la solución de varios problemas de centralidad en árboles. Por ejemplo:

Problema 1. Suponga que varias ciudades están conectadas por un árbol de caminos. El problema es dónde ubicar un local de pizzas, de modo de servir a todas estas ciudades, y minimizar las distancias recorridas de modo que las pizzas siempre lleguen calientes, independientemente de a dónde haya que despacharlas.

En el caso general, cada arco tiene una distancia asociada, y el problema es encontrar el centro.

La excentricidad de cada vértice v es definida como: e(v) = max_{x Î V} {d(v, x)}

Problema 2. Nuevamente tenemos varias ciudades, y ahora se trata de ubicar una planta termoeléctrica en una de ellas, de modo de surtir a todas. Existe un árbol de distribución eléctrica. Cada vértice tiene una demanda c(v). Los arcos pierden fluido eléctrico, de manera que para proveer b unidades de electricidad al extremo v del arco (u, v), debe entregarse g_{(u, v)}(b) unidades en el extremo u. En este caso, la excentricidad de cada vértice v es el número de unidades de electricidad requeridos en v para suplir toda la demanda desde ese vértice.

Problema 3. Suponga que un banco tiene oficinas en todo el país. Dispone de un sistema de distribución de mensajes electrónicos que es un árbol. Para simplificar, consideremos que todo el tráfico va desde un punto de distribución central a los vértices. Se quiere minimizar el máximo tráfico de mensajes transportados por un arco.

Si v es el punto central, el máximo tráfico estará en uno de los arcos (v, x) que salen de v.

Definimos e(v) = max { t_{(v, x)} / x Î Ady(v) }

Ady(v) = conjunto de vértices adyacentes a V ( formalmente: Ady(v) = { u / u Î V y (u, v) Î X} )

Cuando cada vértice recibe una unidad de tráfico, el ejemplo se reduce a encontrar el centroide del árbol.

Existen otros problemas de centralidad en árboles (ver referencias). En muchos de ellos, además de encontrar el punto central, estamos interesados en calcular todas las excentricidades. Por ejemplo, en el problema 2, si se encuentra la ciudad con mínima excentricidad, quizás el alcalde no quiera la planta termoeléctrica en su ciudad. Si se tienen las excentricidades se puede saber cuán preferible es esa ciudad comparada con una segunda, cuyo alcalde está interesado en la ubicación de la planta debido a las plazas de trabajo que creará.

Estudiaremos un algoritmo lineal que permite resolver estos problemas de centralidad en árboles. Veamos alguna terminología adicional.

Definición. Un árbol con raiz T(V, X, r_o) es un árbol tal que:

Definición. Sea un árbol con raiz T(V, X, r_o), y sea v, w, ..., r_o una trayectoria, denotada por p(v, r_o), entonces:

w se llama el padre de v (r_o no tiene padre).

Hijos(v) = Ady(v) - {padre(v)}

l_{(u, v)} = largo del arco (u, v). Además, l_{(u, v)} = l_{(v, u)}

d_{u, z} = å_{xi, xj Î p(u, z)} l_{(xi, xj)}

{c_j: V ® R / j = 1, ..., p} funciones de costo de vértices.

{g_{(u, v)}: R ® R / (u, v) Î X} funciones de costo de lados.
Con la siguiente figura como ejemplo, definimos los conceptos de sub-árbol y rama.

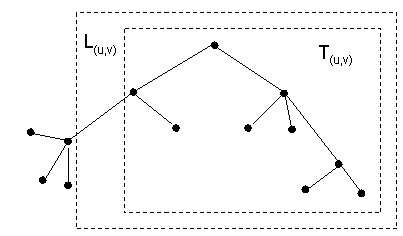
Definición. El sub-árbol T_{(u, v)}( V_{(u, v)}, X_{(u, v)}, v) es un triple donde:

(u, v) Î X

V_{(u, v)} = { w Î V / u Ï p(v, w) } È { v }

X_{(u, v)} = { (x, y) / (x, y) Î X; x, y Î V_{(u, v)} }

Definición. La rama L_{(u, v)}( V_{(u, v)}, X_{(u, v)}, (u, v) ) es un triple donde:

(u, v) Î X

V_{(u, v)} = { w Î V / u Ï p(v, w) } È { v }

X_{(u, v)} = { (x, y) / (x, y) Î X; x, y Î V_{(u, v)} } È { (u, v), (v, u) }

En lo que sigue, simplificaremos la notación así:

T(V, X, r_o) ® T

T_{(u, v)}(V_{(u, v)}, X_{(u, v)}, v ) ® T_{(u, v)}

L_{(u, v)}(V_{(u, v)}, X_{(u, v)}, (u, v)) ® L_{(u, v)}

A cada rama L_{(u, v)} le asociamos un "peso" que llamamos wt(u, v), a partir del cual calcularemos excentricidades.

El cálculo de los pesos se hace a partir de los datos del problema de centralidad específico y con los pesos que ya se han calculado. Los datos del problema pueden ser largos de arcos, funciones de costo en los vértices o funciones de costo en los arcos.

El peso wt(u, v) de una rama L_{(u, v)} es un resumen de la información acerca de la rama.

Definición.

WTS(v) = { wt(v, x) / x Î Ady(v) }

OTHER_WTS(u, v) = WTS(u) - { wt(u, v) }

Antes de que veamos un algoritmo general que nos permitirá resolver los problemas de centralidad en árboles, necesitamos dos pasos previos: estudiar recorridos de árboles y definir algunas funciones.

[anterior] [home] [siguiente]