3.2. Árboles

1. G es un árbol

2. Cualesquiera dos puntos de G se unen por una trayectoria única

3. G es conexo y p = q + 1

4. G es acíclico y p = q + 1

Definición. Un grafo con pesos en los arcos es G = (V, X) con un conjunto {w₁, ..., w_q} asociado a los arcos.

Ejemplo: En una zona aislada existe un conjunto V = {v₁, ..., v_p} de comunidades. También existen caminos entre comunidades, de modo que el grafo es conexo. Ahora se quiere proveerlos de una red eléctrica, con la limitación de que los postes deben ir junto a los caminos (por economizar). Encontrar la red eléctrica que minimice el largo total a establecer.

Pre-solución. Basta un árbol (¿por qué?). Entonces buscamos un subgrafo (árbol) de recubrimiento de G de costo mínimo, donde el costo es la suma de los pesos, que en este caso son los largos de los caminos que serán parte del árbol.

Para encontrar un árbol de recubrimiento mínimo hay varios algoritmos. Mostraremos uno de ellos.

Algoritmo de Prim

Input: Un grafo conexo con pesos G = (V, X), con V = {v₁, ..., v_p}
Output: Un árbol de recubrimiento mínimo T
Método: Expandir el conjunto U Í V desde {v₁} a V usando el arco de mínimo peso de U a V-U.

1. Sea t ¬ v₁, T ¬ Æ, y U ¬ {v₁}

2. Sea w(t, u) ¬ min _{v Î V-U} {w(t, v)}

3. T ¬ T È {e} donde e = tu tiene peso w(t, u)

4. U ¬ U È {u}

5. Si U = V entonces pare.

6. Para cada v Î V-U, sea w(t, v) ¬ min{w(t, v), w(u, v)}

7. Vaya al paso 2

Ejemplo. Con el grafo

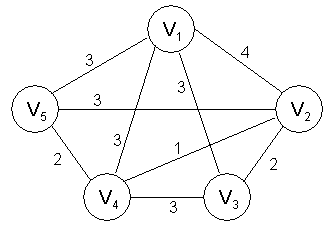
1. t ¬ v₁, T ¬ Æ, y U ¬ {v₁}

2-3. w(t, u) = 3, T ¬ T È {v₁ v₃} (podría haberse elegido cualquiera de v₃, v₄ o v₅)

4-5. U ¬ U È {v₁}, continuamos

6. w(t, v₂) = 2, w(t, v₄) = 3, w(t, v₅) = 3 y continuamos

2-3. w(t, u) = 2 y T ¬ T È {v₂ v₃} = {v₁ v₃, v₂ v₃}

4-5. U ¬ U È {v₂} = {v₁, v₃, v₂} y continuamos

6. w(t, v₄) = 1, y w(t, v₅) = 3 y continuamos

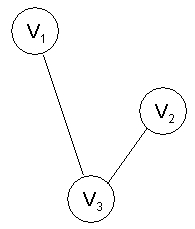
Si continuamos, obtenemos:

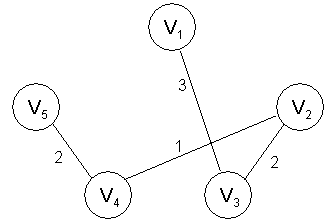
U = {v₁, v₃, v₂, v₄, v₅}

T = {v₁v₃, v₃v₂, v₂v₄, v₄v₅}

Costo total: 3 + 2 + 1 + 2 = 8

El algoritmo de Prim tiene complejidad tiempo O(|V|²).

El problema de encontrar el árbol de recubrimiento mínimo con pesos para digrafos es mucho más difícil. De hecho, no se conoce un algoritmo polinomial para resolver este problema.



[anterior] [home] [siguiente]

---