[anterior]
[home]
[siguiente]
3.1. Modelamiento de redes
Las redes se modelan con grafos. Euler (1707-1782) es considerado el originador de la teoría de grafos, cuando en 1736 resolvió un problema famoso en su tiempo, llamado el problema de los puentes de Königsberg. El río Pregel formaba islas en esa ciudad, y había 7 puentes:
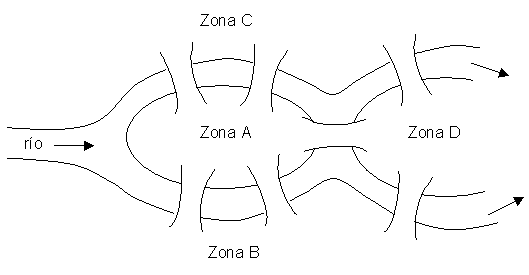
El problema era comenzar encualquiera de las cuatro zonas de tierra (A, B, C o D), atravesar sólo una vez por cada puente y volver al punto de partida.
Para resolver este problema, Euler reemplazó cada zona de tierra por un punto, y cada puente por una línea uniendo los puntos correspondientes y produciendo un multigrafo.
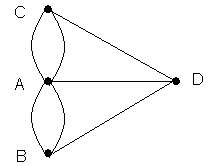
Euler demostró que el problema no tenía solución. Para ello, generalizó el problema y desarrolló un criterio para que un multigrafo dado fuera recorrible de la manera requerida. Este criterio pide que el grafo sea conexo y que cada punto tenga un número par de líneas incidentes. El multigrafo de los puentes de Königsberg es conexo, pero no todo punto tiene un número par de líneas incidentes.
Definición. Un grafo G consiste de un conjunto finito no vacío V = V(G) de p puntos (o vértices, o nodos), y un conjunto X de pares no ordenados de puntos distintos de V. Cada par x = {u, v} de puntos en X es una línea (o arco, o lado) de G y se dice que x une u y v. Escribimos x = uv y decimos que u y v son vértices adyacentes. Un grafo con p puntos y q líneas se llama un grafo (p, q). El grafo (1, 0) es trivial.
Ejercicio. Mostrar que un multigrafo (es decir, varias líneas uniendo dos vértices) no es un grafo.
Definición. Un grafo dirigido (o digrafo) consiste de un conjunto no vacío finito V de puntos y una colección X de pares ordenados de puntos distintos. Los elementos de X son líneas dirigidas o arcos. Un digrafo no puede tener ciclos o arcos múltiples.
Un grafo G es rotulado cuando los p puntos se distinguen uno de otro por nombres tales como v1, v2, ..., vp.
Un subgrafo de G es un grafo que tiene todos sus puntos y líneas en G. Un subgrafo de recubrimiento es un subgrafo que contiene todos los puntos de G.
Definición. Un camino de un grafo G es una secuencia alternada de puntos y líneas v0, x1, v1, ..., vn-1, xn, vn comenzando y terminando en vértices, en que cada línea es incidente con el punto que le antecede y con el que le sigue. Un camino une v0 y vn y puede denotarse también v0, v1, ..., vn (las líneas evidentes). Es una trayectoria si todos los puntos son distintos. Si los n puntos son distintos, n >= 3 y v0 = vn, entonces el camino se llama un ciclo.
El grado de un punto vi en el grafo G, denotado grad vi es el número de líneas incidentes a vi. El primer teorema de teoría de grafos es (Euler):
Teorema. La suma de los grados de los puntos de un grafo G es dos veces el número de líneas:
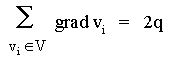
Definiciones. Un grafo completo Kp tiene cada par de sus p puntos adyacentes. Un grafo es conexo si cada par de puntos están unidos por una trayectoria. Un grafo es acíclico si no tiene ciclos.
[anterior]
[home]
[siguiente]