[anterior]
[home]
[siguiente]
1.4.2. Instantes de ocurrencia
Con el ejemplo anterior (ejemplo 8) podemos clarificar las ideas de simulación de eventos discretos. En lugar de avanzar el tiempo del modelo como t, t+1, t+2, ..., si en un momento determinado el tiempo del modelo (también decimos el reloj del modelo) es t, podemos avanzar el tiempo al próximo instante de ocurrencia.
Pensemos, para empezar, que no hay llegada de clientes (es decir, un modelo autónomo). Esto puede ocurrir en la noche, cuando el supermercado ha cerrado la ENTRADA. Entonces, sea t el instante actual, t' el próximo instante de ocurrencia.
t' = t + min {t1, t2, ..., tn, s}
Es decir, t' será el instante actual más el mínimo de los tiempos que quedan para que se produzca un evento. Los t1, t2, ..., tn y s son relojes decrecientes(timers): cuando su valor se hace 0, ocurre un evento. ¿Cómo será la evolución de las variables durante el tiempo? Veamos:
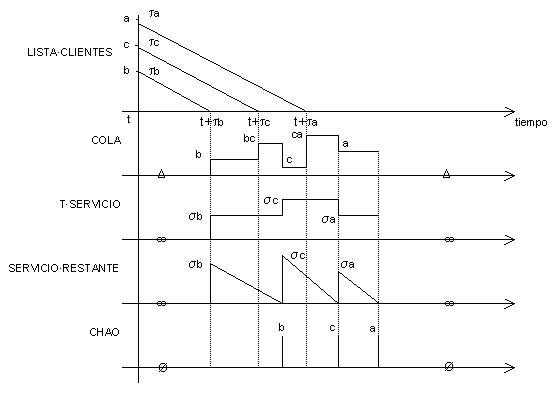
Ejercicio: Hacer el diagrama para la variable OCUPADO.
Ejercicio: Poner, en el eje del tiempo, para cada variable, los instantes de ocurrencia.
Ejercicio: Para el ejemplo, liste los eventos (donde ocurren) y los instantes de ocurrencia correspondientes, ordenadamente en el tiempo.
Examinemos lo que ocurre entre dos instantes de ocurrencia. Por ejemplo, entre (t + tb) y (t + tc) :
- La variable COLA permanece constante (con valor b).
- La variable T·SERVICIO no es muestreada: permanece constante con el último valor de sb.
- La variable SERVICIO·RESTANTE decae linealmente.
- La variable CHAO permanece constante (valor Æ).
En general, entre dos instantes de ocurrencia cualesquiera sucede lo mismo. Por tanto, el tiempo se puede hacer saltar entre instantes de ocurrencia, y esto es la base de la simulación de eventos discretos.
Supongamos que el subprograma que entrega una muestra de la variable aleatoria T·SERVICIO necesite el valor anterior que ella misma generó para dar la muestra. Con este supuesto y recordando que la ENTRADA está cerrada, las variables de estado son:
LISTA·CLIENTES, con valor típico (x, t1), ..., (x, t2).
COLA, con valor típico y1, ..., yn.
T·SERVICIO, con valor típico r.
SERVICIO·RESTANTE, con valor típico s.
Luego, los estados son:
S = ((x1, t1), y1, r, s)
S = ((x2, t2), y1, r, s)
...
Veamos ahora el caso no-autónomo.
La llegada de clientes es un fenómeno externo al modelo, pero también puede modelarse. En un sentido purista, alguien podría afirmar que el modelo, en ese caso, sigue siendo autónomo...
En muchos casos, la llegada de clientes, o mejor dicho, el periodo de tiempo entre llegadas de clientes, puede modelarse por una variable aleatoria, con una distribución acumulada conocida. Sea ENTRE·LLEGADAS esta variable (es decir, si muestreamos ENTRE·LLEGADAS obtenemos la cantidad de tiempo que hay que esperar para que llegue un nuevo cliente a partir del último).
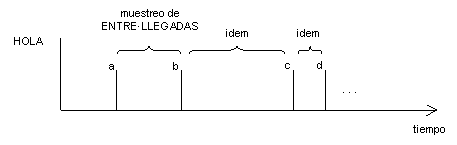
Podemos crear una nueva variable LLEGA, que se inicializa con muestreo de ENTRE·LLEGADAS, y que va decreciendo con el tiempo, de modo que cuandose hace 0, aparece el nuevo cliente, se muestrea ENTRE·LLEGADAS, se asigna a LLEGA, etc. Por tanto, las variables quedan:
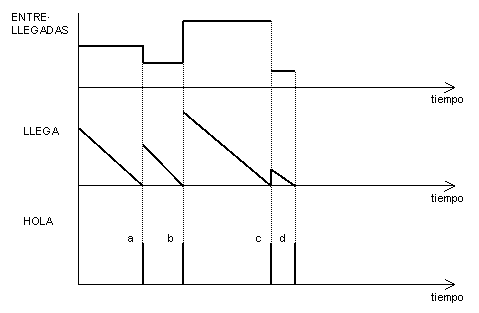
Finalmente, a cada cliente que llega se le asigna un tiempo de compras, muestreando la variable aleatoria T·COMPRAS. Por tanto, todos los eventos son predecibles, que era una de las condiciones de este tipo de simulación.
¿Cuál es ahora el próximo instante de ocurrencia? Si el valor en t de LLEGA es g, entonces:
t' = t + min {t1, t2, ..., tn, s, g}
Ejercicio: Describa todo lo que ocurre con un cliente que llega (cuando g se hace 0).
Ahora estamos en condiciones de ver el procedimiento de eventos discretos.
Necesitamos una estructura de datos para la simulación de eventos discretos: la lista PROXIMOS·EVENTOS. Se trata de una lista ordenada de menor a mayor por el instante de ocurrencia:
PROXIMOS·EVENTOS
| COMPONENTE |
INSTANTE |
| EVENTO·DE·a |
ta |
| EVENTO·DE·b |
tb |
| EVENTO·DE·d |
td |
| ... |
... |
El procedimiento es el siguiente:
* inicialización
1. Poner variable RELOJ con el tiempo de modelo inicial t0.
2. Poner variables S1, S2, ..., Sp con los valores iniciales de las variables de estado (s1, s2, ..., sp).
3. Para las componentes a que tengan un evento, poner el par (EVENTO·DE·a, ta) en la lista PROXIMOS·EVENTOS, en que ta es el instante de ocurrencia calculado. (Ordenar lista).
* avance del tiempo
4. Poner el RELOJ con el ta del primer par en la lista PROXIMOS·EVENTOS.
* transición
5. Realice la transición de estados, extrayendo de la lista PROXIMOS·EVENTOS todos los pares que tengan instante igual a RELOJ, re-programando componentes, cambiando variables, etc. En esta etapa se re-colocan pares (EVENTO·DE·a, ta) en la lista PROXIMOS·EVENTOS, cuidando de ponerlos en el orden apropiado.
* ¿todavía hay una transición con este valor de RELOJ?
6. Si el valor de RELOJ iguala el instante del primer par, vaya a 5.
* chequeo de término
7. Si el valor de RELOJ iguala o excede el instante de término t1, PARE. En caso contrario, vaya a 4.
[anterior]
[home]
[siguiente]



