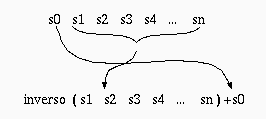
inverso("") -> "".
inverso(s) -> inverso(substring(s, 1, length(s)-1))+ substring(s,0,1)
Temas:
El siguiente programa calcula la función potencia:
double potencia(double x, int n) {
double p= 1.0;
int i= 1;
while (i<=n) {
p= p*x;
i= i+1;
}
return p;
}
double potencia2(double x, int n) {
if (n==0)
return 1.0;
else
return x * potencia2(x, n-1);
}
potencia(5.0,3) -> 125.0
|
5.0*potencia(5.0,2) -> 125.0
|
5.0*potencia(5.0,1) -> 25.0
|
5.0*potencia(5.0,0) -> 5.0
|
1.0
¿Cuantas multiplicaciones realiza esta función cuando se invoca potencia2(3.0, 8)? Se puede deducir que potencia2 realiza el mismo número de multiplicaciones que la versión previa.
La siguiente estrategia permite reducir drásticamente el número de multiplicaciones:
x elevado a n es:
double potencia3(double x, int n) {
if (n==0)
return 1.0;
else if (n%2==0) {
double p= potencia(x, n/2);
return p*p;
}
else {
double p= potencia(x, (n-1)/2);
return x*p*p;
}
}
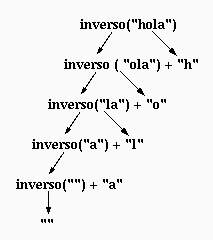
Ejemplo: inverso("hola") -> "aloh".
Solución:
inverso("") -> "".
inverso(s) -> inverso(substring(s, 1, length(s)-1))+ substring(s,0,1)

String inverso(String s) {
if (compare(s,"")==0)
return "";
else
return inverso(substring(s, 1, length(s)-1)) + substring(s, 0, 1);
Ejercicio 2: procedimiento recursivo que despliega un número entero en binario.
Ejemplo: printBin(13) despliega 1101
13 / 2 --> 6 / 2 --> 3 / 2 --> 1 / 2 --> 0
1 0 1 1
void printBin(int n) {
while (n>0) {
print(n%2);
n= n/2;
}
}
Solución correcta:
(0) void printBin(int n) {
(1) if (n==0)
(2) return; // retorno anticipado de un procedimiento
else {
(3) printBin(n/2);
(4) print(n%2);
}
}
En cada invocación recursiva de printBin se crea una nueva variable n para almacenar el parámetro que recibe printBin. Esta variable será visible sólo en esa invocación. Si se invoca recursivamente printBin, esa invocación usará su propio variable n.
Ejecución paso a paso de printBin(13):
(0) n= 13
(1) falso
(3) printBin(6) ->
(0) n= 6
(1) falso
(3) printBin(3) ->
(0) n= 3
(1) falso
(3) printBin(1) ->
(0) n= 1
(1) falso
(3) printBin(0) ->
(0) n= 0
(1) verdadero
(2) return
<-
(4) print(1%2)
<-
(4) print(3%2)
<-
(4) print(6%2)
<-
(4) print(13%2)