Temas:
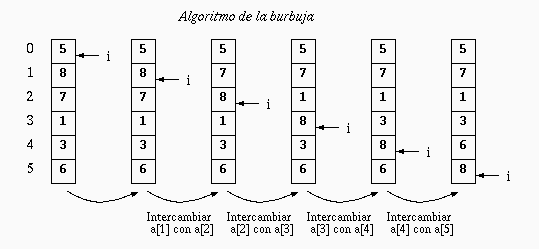
La idea consiste en realizar varios recorridos secuenciales en el arreglo intercambiando los elementos adyacentes que estén desordenados. Como se muestra en la siguiente figura, en la primera iteración se lleva el máximo a su posición definitiva al final del arreglo:

En la segunda iteración se lleva el segundo máximo a su posición definitiva. Y así continúa hasta ordenar todo el arreglo. Observe que si en un recorrido secuencial no se intercambia ningún elemento, el arreglo está ordenado y se puede concluir. El código es entonces:
void burbuja(int[ ] a, int n) {
int iult= n-1;
boolean cambio= true;
while (cambio) {
int i= 0;
cambio= false;
while (i<iult) {
if (a[i]>a[i+1]) {
// intercambiar
int aux= a[i];
a[i]= a[i+1];
a[i+1]= aux;
cambio= true;
}
i= i+1;
}
iult= iult-1;
}
}
Análisis:
Comparación con selección y reemplazo:
Al ordenar arreglos completamente desordenados, el algoritmo de la burbuja toma el doble de tiempo que selección y reemplazo. Sin embargo, puede llegar a ser mucho más eficiente con arreglos semi-ordenados.
El siguiente procedimiento ordena una cola de enteros:
void quicksort(Queue cola) {
// Caso base
if (cola.isEmpty())
return;
// Caso recursivo
int pivot= cola.getInt(); // La cola no esta vacía
Queue menores= new Queue(); // Una cola para los menores que x
Queue mayores= new Queue(); // Una cola para los mayores que x
// Particionamiento
while (!cola.isEmpty()) {
int x= cola.getInt();
if (x>pivot)
mayores.put(x);
else
menores.put(x);
}
quicksort(menores); // Se ordenan los menores recursivamente
quicksort(mayores); // Se ordenan los mayores recursivamente
// Se regresan los valores a la cola inicial
while (!menores.isEmpty())
cola.put(menores.getInt());
cola.put(pivot);
while (!mayores.isEmpty())
cola.put(mayores.getInt());
}
Suponiendo que agregar y extraer elementos de la cola toma tiempo constante, el análisis es el siguiente:
A continuación veremos que la práctica ratifica la teoría.
Comparación de algoritmos
| Número de | Selección | Selección | Burbuja | Quicksort | Quicksort |
|---|---|---|---|---|---|
| elementos | con colas | con arreglos | con arreglos | con colas | con arreglos |
| 100 | 103 miliseg. | 4 miliseg. | 6 miliseg. | 29 miliseg. | 2 miliseg. |
| 500 | 3638 miliseg. | 86 miliseg. | 165 miliseg. | 217 miliseg. | 9 miliseg. |
| 1000 | 20 seg. | 0.3 seg. | 0.7 seg. | 0.6 seg. | 18 miliseg. |
| 2000 | 121 seg. | 1.4 seg. | 2.6 seg. | 1.5 seg. | 43 miliseg. |
| 100000 | más de 3 días | 1 hora | 2 horas | 15 min. | 3.4 seg. |
Observe que para ordenar conjuntos de pocos elementos, quicksort con colas el muchos más lento que selección con arreglos nativos. Sin embargo, con conjuntos de 2000 elementos, ambos se demoran lo mismo. Pero sobretodo, para arreglos de gran tamaño, quicksort con colas es más rápido.
Sin embargo, quicksort con colas todavía no es lo suficientemente rápido. Quicksort con arreglos nativos es aún más rápido. De hecho, es el algoritmo de ordenamiento más eficiente conocido.
Conclusión esencial Para expresar la eficiencia de un algoritmo se usa la notación O(f(n)). Supongamos que dos algoritmos F y G toman tiempo O(f(n)) y O(g(n)) respectivamente. Esto significa que para algún k se tiene:
Si f(n) crece más lentamente que g(n), entonces F es más eficiente que G, sin importar las constantes CF y CG. Por muy grande que sea la constante de F con respecto a la constante de G, tarde o temprano existirá un n a partir del cual F será más rápido que G.
void quicksort(int[] a, int imin, int imax) {
if (imin>=imax)
return;
int k= particionar(a, imin, imax);
quicksort(a, imin, k-1);
quicksort(a, k+1, imax);
}
Finalmente, la función particionar debe entregar la posición en que queda el pivote. Esta es la parte más complicada de quicksort, porque hay que hacerlo sin utilizar un arreglo auxiliar. Además el valor de k es desconocido.
A continuación veremos una versión de particionar que elige como pivote el primer elemento en el intervalo que se va a ordenar (es decir el pivote es a[imin]). Luego, hace variar j desde imin+1 hasta imax. La situación inicial del arreglo es la que se indica en el primer arreglo de la figura. El segundo arreglo muestra la situación antes de comenzar una iteración para un valor determinado de j. Se observa que todos los elementos de a[imin+1] hasta a[k] deben ser menores que el pivote y desde a[k+1] hasta a[j-1] deben ser mayores o iguales al pivote:

Por lo tanto, en cada iteración se compara a[j] con el pivote. Si es menor, se hace crecer k en una posición y se intercambia el elemento k con el elemento j para que se cumpla la situación intermedia en la siguiente iteración.
El tercer arreglo en la figura indica la situación al salir del ciclo. Se observa que el arreglo está prácticamente particionado. Sólo falta colocar el pivote en la k-ésima posición. Esto se logra intercambiando el primer elemento con la k-ésima posición.
int particionar(int[] a, int imin, int imax) {
int ipiv= imin;
int k= imin;
int j= k+1;
while (j<=imax) {
if (a[j]<a[ipiv] ) {
k= k+1;
intercambiar(a, k, j);
}
j= j+1;
}
intercambiar(a, k, ipiv);
return k;
}