Temas:

• Búsqueda binaria recursiva.
• Ordenamiento.
• Ordenamiento por selección y reemplazo.
• Análisis del tiempo de ordenamiento por selección y reemplazo.

Búsqueda binaria recursiva

• Caso base:
  • Si imin>imax, el intervalo es vacío, por lo que x no se encuentra en el arreglo en ese intervalo y se retorna -1.
  • Si no, se calcula icentro=(imin+imax)/2 y se compara x con a[icentro]. Si son iguales, x se encuentra en a[icentro] por lo que se retorna icentro.

• Caso recursivo:
  • Si x<a[icentro] se busca recursivamente en el intervalo [imin,icentro-1].
  • Si x>a[icentro] se busca recursivamente en el intervalo [icentro+1,imax].

    int buscarBinRec(String x, String[] a, int imin, int imax) {
      if (imin>imax)
        return -1;
      int icentro= (imin+imax)/2;
      int comp= compare(x, a[icentro]);
      if (comp==0)
        return icentro;
      if (comp<0)
        return buscarBinRec(x, a, imin, icentro-1);
      else
        return buscarBinRec(x, a, icentro+1, imax);
    }

Ordenamiento

El objetivo de estudiar los algoritmos de ordenamiento es doble. Primero, porque permite ejemplificar la importancia del estudio de la eficiencia de los algoritmos, mostrando que no es intuitivo predecir cuanto tiempo de ejecución toman.

Y segundo, porque los computadores pasan típicamente 50% de su tiempo ordenando (de ahí que los españoles y franceses prefieren usar la palabra ordenador en vez de computador). Parece lógico entonces conocer cuáles son los algortimos que se usan para ordenar.

Hace un año era válido un tercer argumento: si en algún momento un programador necesitaba ordenar un arreglo, tenía que programarlo. A partir de 1999, la versión 1.2 de Java incorpora una clase de biblioteca para ordenar datos de manera eficiente.

Ordenamiento por selección y reemplazo

El problema es que trabajar con colas es doblemente ineficiente:

• Porque accesar los elementos de una cola puede ser 50 veces más lento que accesar los elementos de un arreglo nativo.
• Porque utilizar una segunda cola significa que el algoritmo necesita el doble de la memoria.

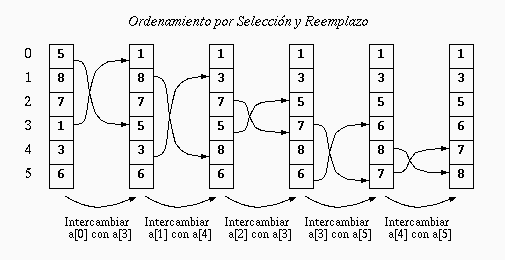
Entonces se procede a intercambiar los valores de a[0] con a[3]. Ahora, a[0] contiene el valor correcto y por lo tanto, nos olvidamos de él. A continuación, el algoritmo ordena el arreglo desde el índice 1 hasta el 5, ignorando a[0]. Por lo tanto, ubica nuevamente la posición del mínimo entre a[1], a[2], ..., a[5] y lo intercambia con el elemento que se encuentra en a[1] como se indica en el segundo arreglo de la figura. Ahora, a[0] y a[1] contienen los valores correctos. Y así el algoritmo continúa hasta que a[0], a[1], ..., a[5] tengan los valores ordenados.

El algoritmo para ordenar un arreglo a de n elementos es:

Realizar un ciclo de conteo para la variable i, de modo que tome valores desde 0 hasta n-1. En cada iteración:

• Suponer que el arreglo se encuentra ordenado desde a[0] hasta a[i-1].
• Ubicar k>=i, tal que a[k]<=a[j], para todo j en [i,n-1].
• Intercambiar los valores de a[k] y a[i].

  void seleccion(int[ ] a, int n) {
    int i= 0;
    while (i<n) {
      // Buscamos la posicion del minimo en a[i], ai+1], ..., a[n-1]
      int k= i;
      int j= i+1;
      while (j<n) {
        if (a[j]<a[k])
          k= j;
        j= j+1;
      }
      // intercambiamos a[i] con a[j]
      int aux= a[i];
      a[i]= a[k];
      a[k]= aux;
      i= i+1;
    }
  }

Se podría introducir una instrucción if para que no se realice el intercambio cuando k==i, pero esto sería menos eficiente que realizar el intercambio aunque no sirva. En efecto, en algunos casos el if permitiría ahorrar un intercambio, pero en la mayoría de los casos, el if no serviría y sería un sobrecosto que excedería con creces lo ahorrado cuando sí sirve.

Análisis del tiempo de ordenamiento por selección y reemplazo

Desarrollando esta inecuación se llega a:

Con A, B y C constantes a determinar. Por lo tanto es fácil probar que:

De la misma forma se puede probar que en el mejor caso y en el caso promedio, el algoritmo también es O(n^2). Por lo tanto:

• Mejor caso: O(n^2)
• Peor caso: O(n^2)
• Caso promedio: O(n^2)

Es fácil probar que el algoritmo basado en colas también es O(n^2) cuando las operaciones agregar y extraer en la cola toman tiempo constante. Esto no es necesariamente cierto con Queue, pero sí es cierto si la cola se implementa con arreglos nativos o con las listas enlazadas que veremos al final del curso.

La siguiente es una comparación empírica de los tiempos de ejecución de ambos algoritmos:

Se puede observar que el uso de arreglos nativos es unas 50 veces más eficiente que la cola. Sin embargo, el algoritmo de ordenamiento por selección y reemplazo sigue siendo O(n^2) y por lo tanto es ineficiente.

En efecto, si consideramos el problema de la clase pasada en que se necesitaba ordenar para luego realizar búsquedas eficientes, esta solución no sirve, porque el ordenamiento tiene un sobrecosto que excede las ganancias de la búsqueda binaria.