Lunes 8 de Noviembre

Matrices

Objetivos:

Temas:

Azúcar sintáctico

Algunos de los patrones de programación se repiten tan frecuentemente que los lenguajes de programación incluyen formas sintácticas que son abreviaciones para estos patrones. El único objetivo de estas abreviaciones es brindar un mecanismo para escribir menos código:

Ejemplo: cálculo del factorial. 

    double fact(int n) {
      int i;
      double f= 1;
      for (i=1; i<=n; i++)
        f= f*i;
      return f;
    }

El tipo de datos matriz

Las matrices son un caso especial de arreglos. Se distinguen de los arreglos tradicionales en que se especifican 2 índices en vez de uno. Las operaciones que se pueden realizar con una matriz son:

Ejemplo Significado Sintaxis
double[][] m= new double[n][p]; Construye una matriz de n x p new tipo[filas][cols]
m[i][j]= 5.2; Almacena 5.2 en la fila i, columna j matriz[[fila][col]
double x= m[i][j]; entrega el valor almacenado en i,j matriz[[fila][col]= exp;

Para leer una matriz 10 x 20 se usa:

    int n= 10;
    int p= 20;
    TextReader lect= new TextReader("matriz.dat");
    double[][] m= new double[n][p];
    for (int i= 0; i<n; i++)
      for (int j= 0; j<p; j++)
        m[i][j]= lect.readDouble();
El mismo patrón se puede usar para escribir la matriz. Es muy importante darse cuenta que el patrón anterior recorre la matriz por filas. Es decir que el archivo debe contener primero los valores para la primera fila, luego los valores para la segunda fila, etc.

El siguiente código despliega el contenido de la matriz pero por columnas:

    for (int j= 0; j<p; j++)
      for (int i= 0; i<n; i++)
        print(m[i][j])
Primero despliega la primera columna, luego la segunda, etc. Por supuesto el programa debería colocar las columnas en distintas líneas:

    for (int j= 0; j<p; j++) {
      for (int i= 0; i<n; i++)
        print(m[i][j])
      println();
    }

Multiplicación de matrices

Supongamos que tenemos dos matrices a y b de n x p y de p x q respectivamente. Podemos calcular c= a*b, de n x q, mediante:

    double c= new double[n][q];
    for (int i= 0; i<n; i++)
      for (int j= 0; j<q; j++) {
        c[i][j]= 0.0;
        for (int k= 0; k<p; k++)
          c[i][j]+= a[i][k]*b[k][j];
      }

Resolución de sistemas de ecuaciones lineales

Un sistema de ecuaciones lineales puede ser formulado mediante matrices a través de la siguiente ecuación:

El mismo problema puede ser formulado matricialmente de la siguiente forma:

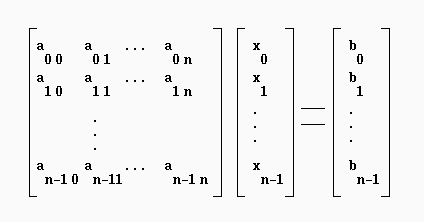
Para encontrar la solución es necesario triangularizar primero la matriz de modo de llegar a:

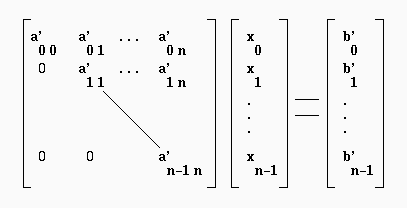
El programa que triangulariza la matriz es:

    void triangularizar(double[][] a, double[] b, int n) {
      for(int i=0; i<n; i++) {
        // dividir fila i por primero de fila i
        double prim= a[i][i];
        for (int j=i; j<n; j++)
          a[i][j] /= prim;
        b[i] /= prim;

        // file j = file j - fila i * primero de fila j
        for(int j= i+1; j<n; j++) {
          prim= a[j][i]
          for(int k= i; k<n; k++)
            a[j][k] -= a[i][k]*prim;
          b[j] -= b[i]*prim;
        }
      }
    }
Observación: este programa no funciona si el primero se hace 0. Mejore esta solución intercambiando la fila i por aquella que tenga el mayor valor absoluto en la columna i.

El problema de resolver un sistema de ecuaciones se puede abstraer en el siguiente procedimiento:

    void resolver(double a[][], double[] b, double[] x, int n) {
      triangularizar(a, b, n);

      // cálculo de los resultados
      for (int i= n-1; i>=0; i--) {
        double sum= 0.0;
        for (int j= i+1; j<n; j++)
          sum += x[j]*a[i][j];
        x[i]= (b[i]-sum)/a[i][i];
      }
    }