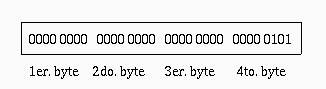
Temas:
Un computador tiene por ejemplo 32 mega bytes de memoria (MB). Esto significa que tiene 32*1024*1024 bytes (o 32*1024*1024*8 bits). A principios de los 80s, los PCs tenían muy poca memoria: 64 kilo bytes (KB), es decir 64*1024 bytes. En computación los kilos corresponden a 1024 (y no 1000) y los megas a 1024 kilos. Esto se debe a que es más fácil construir computadores que tengan una capacidad de memoria que sea múltiplo de 1024 o 1024*1024.
Una variable entera (int) está formada por 4 bytes, es decir 32 bits. Estos 32 bits representan el valor almacenado por esa variable en binario. Por ejemplo:
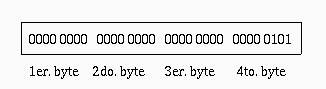
El valor representado por esta variable es:
1*2^2 + 0*2^1 + 1*2^0
En donde x^y se usa acá como una abreviación de x elevado a y.En general, una variable entera x está formada por 32 bits que denotaremos x31, x30, ... , x2, x1 y x0. El valor numérico representado por la variable x está dado por el siguiente cálculo:
x31*2^31 + x30*2^30 + ... + x2*2^2 +x1*2^1+ x0*2^0
yi= 1 si xi==0
0 si xi==1
valor(x) = - (valor(y) + 1)
Se dice que y es el complemento de x.
Ejemplos:
Una variable entera (int) siempre utiliza 32 bits, aún cuando el número sea pequeño. Por otra parte, no es capaz de almacenar números demasiado grandes (en valor absoluto).
Valores máximos y mínimos
Máximo= valor(011...111111)= 2^31-1
Mínimo= valor(100...000000)= -2^31
Por lo tanto, con un int se pueden almacenar números de 9 dígitos aproximadamente.
Tarea: juegue con el programa Jalisco ingresando los números 2147483646 y 2147483647. ¡Explique qué sucedió!
Ejercicios:
| tipo | número | rango |
|---|---|---|
| de bits | representado | |
| int | 32 | [-2^31,2^31-1] |
| short | 16 | [-2^15,2^15-1] |
| byte | 8 | [-2^7,2^7-1] |
| long | 64 | [-2^63,2^63-1] |
Una variable real (double) está formada por 8 bytes, es decir el doble de un entero. En ella se almacenan números reales en formato binario. Por ejemplo, el número:
representa en decimal al número:
Los primeros computadores almacenaban los números reales en una formato llamado punto fijo, en donde se destinaba una cantidad fija de bits para la parte entera (por ejemplo 32 bits) y el resto a la parte fraccionaria. Por lo tanto, el número anterior sería representado en 64 bits como:
00000000 00000000 00000000 00001101 . 10100000 00000000 00000000 00000000
En esta representación, el punto que separa la parte entera de la parte fraccionaria, siempre se ubica en una posición fija y de ahí el nombre de esta representación.
El problema de esta representación es que el rango de valores representables es el mismo de los números enteros. Se necesitaba un mecanismo que aumentara el rango de números representables. La forma de hacerlo fue destinar una parte de los bits a indicar la posición del punto. Y este formato paso a llamarse punto flotante.
Representación en punto flotante
Un número real se almacena en una variable especificando 3 componentes: el signo (+ o -), la mantisa y el exponente. Por ejemplo, el número 11 se representa como:
¿Qué número es el siguiente?
Otros ejemplos:
| signo | mantisa | exponente | en binario | en decimal |
|---|---|---|---|---|
| + | 1000... | 100 | 1 seguido | 2^99 |
| de 99 ceros | ||||
| + | 1010... | 0 | 0.1010 | 0.5+0.125 (0.625) |
| + | 1000... | -3 | 0.0001 | 2^(-4) (0.0625) |
En una variable de tipo double se destina 1 bit para el signo, 11 bits para el exponente y 52 bits para la mantisa.
Valores máximos y mínimos
Máximo en valor absoluto: 2^1023
Valor más pequeño: 2^(-1024)
La ventaja de esta representación es que se alcanza un rango de representación mucho más grande de lo que sería posible con 64 bits.
Precisión y error de representación
La desventaja es que los números se almacenan con una precisión limitada. Esto significa que un número que requiera 100 bits de mantisa será aproximado a uno que solo ocupa 52, introduciéndose entonces un error de representación.
El error que se comente se puede visualizar mejor en base 10. El error que comete es como cuando el siguiente número:
1234567890123456789012345678901234567890
se aproxima al siguiente valor:
123456789012345*10^25
Es decir, solo se reprentan 15 dígitos de los 40 iniciales. El error absoluto que se comete es:
6789012345678901234567890
que parece enorme, pero lo que importa es el error relativo que es ~10^(-15) que es bajísimo y para la mayoría de las aplicaciones numéricas es insignificante. Pero es un error que conviene tener presente.
Observación: además del tipo double existe el tipo float
| tipo | tamaño | mantisa | exponente | rango | precisión |
|---|---|---|---|---|---|
| en bits | en bits | en bits | representado | en dígitos | |
| double | 64 | 52 | 11 | ~ [-10^300,10^300] | ~ 15 |
| float | 32 | 24 | 7 | ~ [-10^33,10^33] | ~ 7 |
Tarea opcional:
Muestre que el número 0.3 no es representable en forma exacta en una variable de tipo double.
Indicación:
Para obtener la representación de un número en el rango [0,1[ como 0.6875 proceda de la siguiente forma: