Temas:
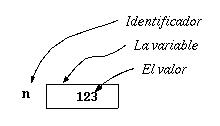
int n= 123;

A continuación presentaremos algunas nociones importantes para comprender el concepto de recursividad.
Tiempo de vida de una variable:
El tiempo de vida se refiere al intervalo de tiempo que trascurre desde que se crea la variable hasta que se destruye. En Java, una variable se crea en el momento que se ejecuta su declaración y se destruye cuando finaliza el bloque de instrucciones en donde fue declarada. Por ejemplo:
if ( ... ) {
println( ... );
int n= 123; // (A)
...
n= ...; // (B)
...
} // (C)
Un mismo identificador se puede usar para nombrar varias variables distintas. Por ejemplo en el siguiente código:
{
int x= a+b;
... x ...
}
{
int x= fun(a,b);
... x ...
}
Incluso, la declaración de una variable puede aparecer una sola vez en el programa, pero aún así servir para identificar varias variables durante la ejecución del programa. Esto se aprecia en el siguiente ciclo:
while ( ... ) {
...
double x= 3.14; // (A)
...
x= ...;
...
} // (C)
Los parámetros de una función también son variables. Se crean en el momento que la función es invocada y se destruyen al finalizar la ejecución de la función. Por ejemplo, la siguiente función calcula el máximo común divisor:
int mcd(int x, int y) {
while (x!=y) {
if (x>y)
x= x-y;
else
y= y-x;
}
return x;
}
int a= 15;
println( mcd(a, 21) );
println( mcd(25, a) );
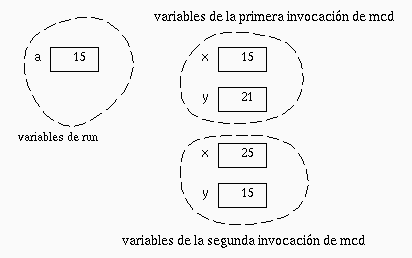
Observe en la figura que durante la ejecución del programa se crean dos variables con nombre x. Esto no constituye ninguna confusión en el momento de accesar la variable x, puesto que ambas variables tienen tiempo de vista disjuntos.
Observe también, que la función mcd modifica los parámetros x e y sin modificar el valor de la variable a en ninguna de las invocaciones. Una función no puede producir efectos laterales sobre las variables que se especifiquen como argumentos durante la invocación. Sin embargo, una función sí puede producir efectos laterales sobre los objetos que se pasen como argumentos en la invocación (como por ejemplo un arreglo).
Existen casos que sí existen varias variables con el mismo nombre en un mismo instante. Por ejemplo, consideremos el siguiente programa:
int x= 105;
println( mcd(210, x) );
Alcance de una variable:
El alcance de una variable es el conjunto de instrucciones en la que esa variable es visible por medio de su identificador. En Java, el alcance de una variables está delimitado por la primera instrucción que sigue a su declaración en el programa, hasta el final del bloque en donde fue declarada. Por ejemplo en:
void run() {
int x= 105; // (A)
println( mcd(210, x) );
} // (B)
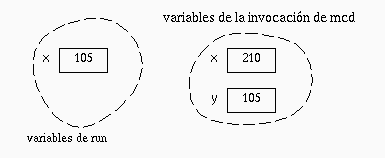
Es importante entender la diferencia entre alcance y tiempo de vida de una variable. En el ejemplo anterior, mientras se ejecuta la función mcd, la variable x del procedimiento run continúa existiendo, a pesar de que no es visible desde mcd. Si una variable no es visible, no necesariamente ha sido destruida. En cambio, si una variable fue destruida, esa variable no es visible.
El siguiente programa calcula la función potencia:
double potencia(double x, int n) {
double p= 1.0;
int i= 1;
while (i<=n) {
p= p*x;
i= i+1;
}
return p;
}
double potencia2(double x, int n) {
if (n==0)
return 1.0;
else
return x * potencia2(x, n-1);
}
potencia(5.0,3) -> 125.0
|
5.0*potencia(5.0,2) -> 125.0
|
5.0*potencia(5.0,1) -> 25.0
|
5.0*potencia(5.0,0) -> 5.0
|
1.0
¿Cuantas multiplicaciones realiza esta función cuando se invoca potencia2(3.0, 8)? Se puede deducir que potencia2 realiza el mismo número de multiplicaciones que la versión previa.
La siguiente estrategia permite reducir drásticamente el número de multiplicaciones:
x elevado a n es:
double potencia3(double x, int n) {
if (n==0)
return 1.0;
else if (n%2==0) {
double p= potencia(x, n/2);
return p*p;
}
else {
double p= potencia(x, (n-1)/2);
return x*p*p;
}
}
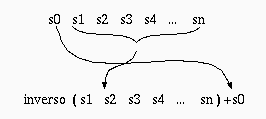
Ejemplo: inverso("hola") -> "aloh".
Solución:
inverso("") -> "".
inverso(s) -> inverso(substring(s, 1, length(s)-1))+ substring(s,0,1)
String inverso(String s) {
if (compare(s,"")==0)
return "";
else
return inverso(substring(s, 1, length(s)-1)) + substring(s, 0, 1);
}

Ejercicio 2: procedimiento recursivo que despliega un número entero en binario.
Ejemplo: printBin(13) despliega 1101
13 / 2 --> 6 / 2 --> 3 / 2 --> 1 / 2 --> 0
1 0 1 1
void printBin(int n) {
while (n>0) {
print(n%2);
n= n/2;
}
}
Solución correcta:
(0) void printBin(int n) {
(1) if (n==0)
(2) return; // retorno anticipado de un procedimiento
else {
(3) printBin(n/2);
(4) print(n%2);
}
}
En cada invocación recursiva de printBin se crea una nueva variable n para almacenar el parámetro que recibe printBin. Esta variable será visible sólo en esa invocación. Si se invoca recursivamente printBin, esa invocación usará su propio variable n.
Ejecución paso a paso de printBin(13):
(0) n= 13
(1) falso
(3) printBin(6) ->
(0) n= 6
(1) falso
(3) printBin(3) ->
(0) n= 3
(1) falso
(3) printBin(1) ->
(0) n= 1
(1) falso
(3) printBin(0) ->
(0) n= 0
(1) verdadero
(2) return
<-
(4) print(1%2)
<-
(4) print(3%2)
<-
(4) print(6%2)
<-
(4) print(13%2)