Cálculo de las raíces de una función

Objetivos: Mostrar una primera aplicación numérica de la computación, resaltando la problemática de trabajar con números reales.

Temas:

El problema del cálculo de raíces

Las raíces de una función y=f(x) son los valores x en los cuales f(x) se hace 0. En algunos casos, la función f tiene una forma tal que el problema se puede resolver algebraicamente. Es el caso de los polinomios de grado 2, e incluso los polinomios de grado 3 y 4. Sin embargo, en la mayoría de los casos, el problema sólo tiene solución numérica.

Esto significa que hay que usar el computador para encontrar los valores numéricos de las raíces. No es posible, encontrar una fórmula algebraica que entregue las soluciones.

A continuación veremos un programa en Java que permite resolver numéricamente el problema de la búsqueda de las raíces de una función cualquiera. Para precisar aún más el problema la función f será un polinomio de grado 5 (pero podría reemplazarse por cualquier otra función continua):

    f(x)= x^5-5*x^4-x^3+5*x^2-3*x+15
Para poder resolver el problema se necesita que el usuario suministre dos valores de x para los cuales la función toma signos opuestos. Para obtener estos valores es útil que el usuario del programa grafique la función (ver clase auxiliar anexa) como se indica en la siguiente figura:

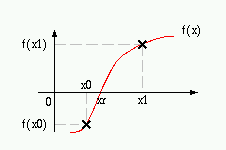
El gráfico le indicará más o menos el intervalo en donde se puede encontrar una raíz, pero no el valor preciso. Este intervalo es [x0,x1].

Para el caso del polinomio puesto como ejemplo, se tiene que: 

    f(3)= -138
    f(8)= 12087
Entonces entre x0=3 y x1=8 tiene que existir una raíz xr para esta función (la condición es que la función sea continua). El problema consiste entonces en encontrar xr.

El programa tendrá la siguiente forma:

class Raices extends Program {
  double eval(double x) {
    double y= pow(x,5)-5*pow(x,4)-pow(x,3)+5*x*x-3*x+15;
    return y;
  }
  void run() {
    print("x0= ? ");
    double x0= readDouble();
    print("x1= ? ");
    double x1= readDouble();
    ... ubicar xr tal que eval(xr)=0 ...
    println(xr);
  }
}
El programa utiliza evalpara evaluar la función en un valor espécifico de x. Es cómodo definir esta función primero, porque de esta forma se puede cambiar fácilmente para calcular la raíz de una nueva función, y segundo porque se utiliza varias veces dentro de run.

Método de la bisección

La idea es especular que la raíz se encuentra en xr=(x0+x1)/2 y evaluar la función para ver que tan lejos se estuvo:

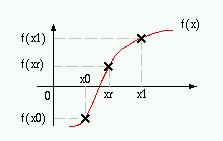
En seguida se procede así:

El proceso termina cuando f(xr)=0.

    double y0= eval(x0);
    double y1= eval(x1);
    double xr= (x0+x1)/2;
    double yr= eval(xr);
    while (yr!=0) {
      if (y0<0 && yr<0 || y0>0 && yr>0) {
        x0= xr;
        y0= yr;
      }
      else {
        x1= xr;
        y1= yr;
      }
      xr= (x0+x1)/2;
      yr= eval(xr);
    }
Esta solución matemáticamente es correcta, pero no computacionalmente. El problema es que la convergencia hacia una raíz puede tomar mucho tiempo. Además es muy probable que nunca se encuentra un valor x tal que la función se haga exactamente 0. Este es el caso en que la raíz es un número irracional, porque estos números no son representables en el computador. Después de un buen rato, el proceso iterativo quedará en un ciclo infinito en el que x0 es igual a x1 e igual a xr, pero f(xr) no será 0.

Por lo tanto en la práctica, es necesario pedirle al usuario que indique un error máximo para la solución. El proceso iterativo termina cuando se encuentre un valor aproximado cuyo error es inferior al error suministrado.

El problema se reduce a encontrar xr tal que:

abs(xr-raíz de f)<= error máximo

La parte que falta del programa será entonces:

    print("error= ?");
    double error= readDouble();
    double y0= eval(x0);
    double y1= eval(x1);
    double xr= (x0+x1)/2;
    double yr= eval(xr);
    int cont= 0;
    while (abs(x0-x1)>error) {
      if (y0<0 && yr<0 || y0>0 && yr>0) {
        x0= xr;
        y0= yr;
      }
      else {
        x1= xr;
        y1= yr;
      }
      xr= (x0+x1)/2;
      yr= eval(xr);
      cont= cont+1;
    }
    println("raiz aprox.= "+xr);
    println("f(raiz)= "+yr);
    println("iteraciones= "+cont);
Resultados con error de 10^(-10):

    x0= ? 3
    x1= ? 8
    error= ? 0.0000000001
    raiz aprox.= 5.000000000007276
    f(raiz)= 4.343746695667505E-9
    iteraciones= 36
Resultados con error de 10^(-20):

    x0= ? 3
    x1= ? 8
    error= ? 0.00000000000000000001
    ... no termina ...
Conclusión esencial: en los problemas que se resuelven numéricamente, lo usual es que se llegue a soluciones aproximadas. Es imposible llegar a soluciones exactas, debido a que el computador maneja los números en forma imprecisa.

En la práctica no se necesitan soluciones exactas, porque típicamente las constantes que aparecen en una función provienen de mediciones experimentales que son también imprecisas. Por ejemplo, es imposible construir un termómetro que sea capaz de medir con más de 4 dígitos de precisión. Por lo tanto, en cualquier problema en donde intervengan temperaturas, no tiene sentido especificar un error de 0.00001.

Método de la interpolación

El método anterior puede ser optimizado para lograr que el programa converja más rápidamente. La idea es que en pequeños tramos las funciones se comportan como líneas rectas. A partir de este supuesto, como se indica en la siguiente figura, se puede trazar una línea recta entre (x0,y0) y (x1,y1), y estimar x2 como la raíz de esta línea recta.

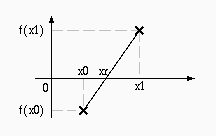
El punto de la intesección está dado por:

x2= (x0*y1-x1*y0)/(y1-y0)

A continuación se descarta (x0,y0), se calcula y2=f(x1) y se determina x3 como raíz de la línea recta que pasa por (x1,y1) y (x2,y2). Y así en adelante, hasta que yn sea menor que un error suministrado por el usuario.

El programa se modifica de la siguiente forma:

    print("error= ? ");
    double error= readDouble();
    double y0= eval(x0);
    double y1= eval(x1);
    int cont= 0;
    while (abs(y1)>error) {
      double xn= (x0*y1-x1*y0)/(y1-y0);
      x0= x1;
      y0= y1;
      x1= xn;
      y1= eval(x1);
      cont= cont+1;
    }
    println("raiz aprox.= "+x1);
    println("f(raiz)= "+y1);
    println("iteraciones= "+cont);
Observe que en este caso, el criterio de detención es distinto del método anterior, porque el error se estima en el eje y, y no en el eje x.

Resultados:

x0= ? 3
x1= ? 8
error= ? 0.0000000001
raiz aprox.= 1.5174899135519972
f(raiz)= -6.732392421326949E-13
iteraciones= 10
El resultado es que el método tarda sólo 10 iteraciones en encontrar una solución. Incluso, esta solución es mejor que la del método anterior, puesto que la evaluación de la función es más cercana a 0 que la anterior.

Las ventajas de este esquema son que (i) converge más rápidamente y (ii) no necesita puntos en que la función se evalúe con signos opuestos.

Las desventajas es que (a) el error está referido al eje y, no a la raíz como debería ser, (b) no se tiene control sobre el intervalo en el que se buscará la solución, y (c) no se tiene garantía de que el método converja a un cero de la función, aunque por lo general sí converge.