Temas:
La abstracción es importante para poder disminuir la complejidad de los problemas que se enfrentan. Sin embargo, también es útil conocer aspectos de la implementación de los tipos de datos con los que se trabaja y por ello estudiamos como se representaban los números reales. Esto nos permite entender mejor sus limitaciones, como el número finito de decimales que puede almacenar.
En este capítulo estudiaremos las técnicas que se usan para implementar los tipos de datos abstractos como las pilas, colas, arreglos asociativos y otros. Es decir definiremos (implementaremos) estas clases.
La estructura de datos de uso más frecuente es el arreglo. Las pilas, colas y arreglos asociativos se implementan fácilmente por medio de arreglos nativos. Sin embargo, el resultado presenta serias deficiencias que resolveremos por medio de dos nuevas estructuras de datos: las listas enlazadas y los árboles.
Ejemplo: Implementación de una pila de enteros
El problema reside en donde almacenar los elementos de la pila. Lo más fácil es almacenarlos en un arreglo:
class Pila extends Program {
int a[];
int tope;
int max;
Pila() {
max= 100;
a= new int[max];
tope= 0;
}
void push(int x) {
if (tope>=max)
fatalError("desborde de pila");
a[tope]= x;
tope++;
}
int popInt() {
if (tope==0)
fatalError("pila vacia");
tope--;
return a[tope];
}
boolean isEmpty() {
return tope==0;
}
}
El problema de esta implementación es que si se llena el arreglo, hay que terminar el programa con un mensaje de error. Es decir la pila queda limitada a 100 elementos o el tamaño que se elija.
Una mejor implementación de una pila debería hacer crecer automáticamente el arreglo cuando se excede su tamaño. Por ejemplo se podría hacer crecer el tamaño en un factor 2. Ahora el problema es que si en algún momento se agrega un millón de elementos en la pila, la pila ocupará para siempre un millón enteros de la memoria del computador, incluso si sólo contiene unos cuantos enteros.
class Eslabon {
...
Eslabon prox;
}
Junto con poseer una referencia del próximo eslabón en la cadena, se
colocan variables de instancia para almacenar datos concerniente
al problema que se pretende resolver. Por ejemplo, para implementar
la pila se puede colocar un entero en cada eslabón de la cadena:
class Eslabon {
int x;
Eslabon prox;
Eslabon(int x, Eslabon prox) {
this.x= x;
this.prox= prox;
}
}
class Pila extends Program {
Eslabon primero= null;
void push(int x) {
primero= new Eslabon(x, primero);
}
int popInt() {
if (primero==null)
fatalError("pila vacia");
int tope= primero.x;
primero= primero.prox;
return tope;
}
}
| Ejemplo | Significado | Declaración |
|---|---|---|
| StringQueue q= new StringQueue(); | Construye una cola de strings vacía | StringQueue() |
| q.put("hola"); | Agrega el string "hola" al final | void put(String s) |
| String s= q.getString() | extrae y entrega el primer elemento de la cola | String getString() |
| int l= q.size() | entrega la cantidad de elementos de la cola | int size() |
Se puede usar un arreglo para almacenar los elementos de la cola, pero se presentan las mismas deficiencias de la pila implementada con arreglos.
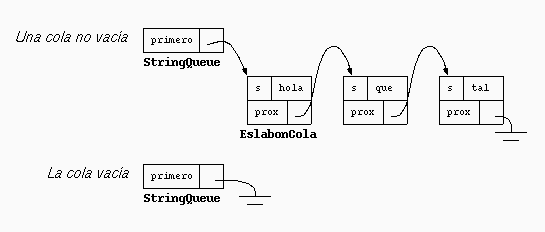
La estructura de datos más conveniente para implementar una cola es la lista enlazada, al igual que la pila. La siguiente figura muestra la estructura de una cola en la que se han encolado los strings "hola", "que" y "tal":

La estructura de los eslabones queda representada por medio de la siguiente clase:
class EslabonCola {
String s;
EslabonCola prox;
EslabonCola(String s, EslabonCola prox) {
this.s= s;
this.prox= prox;
}
}
class StringQueue extends Program {
EslabonCola primero;
... // Los métodos getString, put y size
}
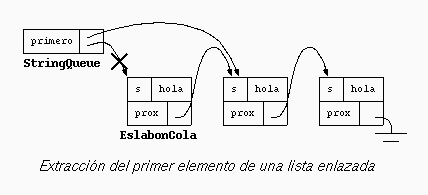
String getString() {
String s= primero.s;
primero= primero.prox;
return s;
}
Observe que si la cola tenía exactamente un eslabón, después de extraerlo de la cola, la lista enlazada queda sin eslabones.
int size() {
int cont= 0;
EslabonCola e= primero;
while (e!=null) {
e= e.prox;
cont= cont+1;
}
return cont;
}
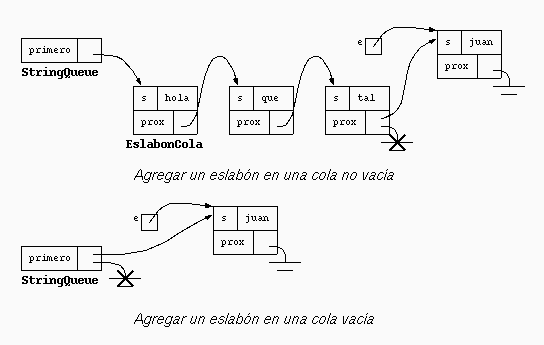
void put(String s) {
if (primero==null)
primero= new EslabonCola(s, null);
else {
EslabonCola e= primero;
while (e.prox!=null)
e= e.prox;
e.prox= new EslabonCola(s, null);
}
}
Análisis del tiempo de ejecución de cada operación:
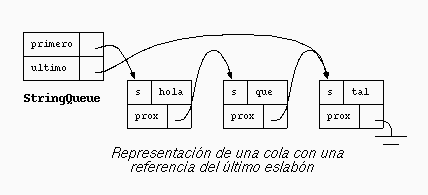
class StringQueue extends Program {
EslabonCola primero;
EslabonCola ultimo;
... // Los métodos getString, put y size
}
void put(String s) {
EslabonCola e= new EslabonCola(s, null);
if (primero==null)
primero= ultimo= e;
else {
ultimo.prox= e;
ultimo= e;
}
}
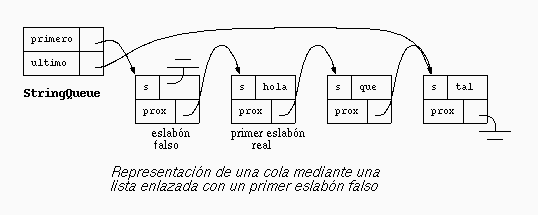
class StringQueue extends Program {
EslabonCola primero;
EslabonCola ultimo;
StringQueue() {
primero= ultimo= new EslabonCola(null, null); // eslabón falso
}
String getString() {
if (primero.prox==null)
fatalError("Cola vacía");
String s= primero.prox.s;
primero.prox= primero.prox.prox;
return s;
}
int size() {
int cont= 0;
EslabonCola e= primero.e;
while (e!=null) {
e= e.prox;
cont++;
}
return cont;
}
void put(String s) {
ultimo.prox= new EslabonCola(s, null);
ultimo= ultimo.prox;
}
}
| Ejemplo | Significado | Declaración |
|---|---|---|
| Map m= new Map(); | Construye un arreglo asociativo con llaves enteras, inicialmente vacío | Map() |
| m.put(2, "hola"); | Asocia el entero 2 con el string "hola" | void put(int ll, String s) |
| String s= (String)m.get(2); | entrega el objeto asociado a la llave 2 ("hola"). Si la llave no posee valor asociado se produce un error. | String getString(int ll) |
| if (m.isMapped(2)) ... | entrega verdadero si la llave 2 tiene un valor asociado. | boolean isMapped(int ll) |
| m.remove(2) | elimina la asociación (2,...) del arreglo asociativo. | void remove(int ll) |
Por simplicidad, esta versión restringida de Map está restringida sólo a valores de tipo String. Más tarde veremos como enriquecer esta clase para cualquier tipo de valores (pero no cualquier llave). Por lo tanto las siguientes operaciones no estarán implementadas:
m.put(1, 3); // no implementada
m.put(1, 3.14); // no implementada

En la figura se observa la estructura de una arreglo asociativo que posee las asociaciones (2, "hola"), (5, "que") y (3, "tal").
En el objeto que representa el arreglo asociativo se coloca una referencia del primer eslabón de la lista enlazada. Por conveniencia, se incluye un eslabón falso para que la lista nunca esté vacía. En este caso no es útil tener una referencia del último eslabón, porque ninguna operación requiere agregar algún eslabón al final de la lista enlazada.
Observe que el orden en que se organiza la lista enlazada es irrelevante. El eslabón que contiene la llave 2 podría haber quedado perfectamente después del eslabón de la llave 5 sin alterar el contenido formal del arreglo asociativo. El orden en que quedarán almacenadas las llaves depende únicamente del orden en que se hagan las asociaciones.
Por lo tanto, la estructura de representación de la clase Map y la clase EslabónM es la siguiente:
class Map extends Program {
EslabonM primero= new EslabonM(0, null, null);
... la implementación de la operaciones de Map ...
}
class EslabonM {
int llave;
String val;
EslabonM proximo;
EslabomM(int llave, String val, EslabomM proximo) {
this.llave= llave;
this.val= val;
this.proximo= proximo;
}
}
String getString(int llave) {
EslabonM e= primero.proximo;
while (e!=null) {
if (e.llave==llave)
return e.val;
e= e.proximo;
}
fatalError("No se encontro la llave "+i); // termina la ejecución!
return null; // para que pase la compilacion
}
También se necesita hacer este mismo recorrido con la operación put. Si la llave existe se modifica el valor en el mismo eslabón. Si la llave no existía previamente en la lista enlazada, se crea un nuevo eslabón para esa llave y se agrega por conveniencia justo después del eslabón falso:
void put(int llave, String val) {
EslabonM e= primero.proximo;
while (e!=null) {
if (e.llave==llave) { // la llave existe
e.val= val; // cambiamos su valor
return; // y retornamos
}
e= e.proximo;
}
// la llave no existía previamente
// Creamos un nuevo eslabon y lo agregamos entre el eslabon
// falso y el segundo eslabon
e= new EslabonM(llave, val, primero.proximo);
primero.proximo= e;
}

Ejercicio: Verifique que las dos operaciones funcionan correctamente cuando el arreglo asociativo se encuentra vacío (cuando la lista enlazada sólo contiene el eslabón falso).
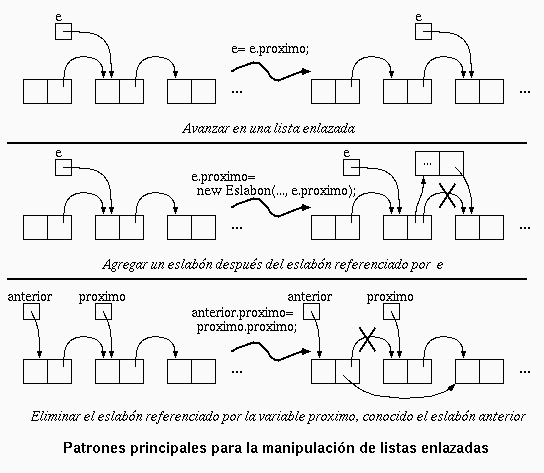
El primer intento de implementación que viene a la mente consiste en usar el patrón de recorrido de los eslabones para buscar la llave que se desea eliminar. Sin embargo, este patrón no sirve porque cuando se encuentre la llave, la variable de instancia prox que hay que modificar se encuentra en el eslabón visitado en la iteración anterior. Pero este eslabón ya se visitó y no es posible volverlo a recorrer si comenzar por el primer eslabón.
Para resolver el problema, modificamos ligeramente el patrón de recorrido de modo de mantener en la variable anterior el eslabón visitado en la iteración anterior. La siguiente figura muestra cómo realizar la eliminación del eslabón utilizando la variable anterior:

El código para eliminar una llave del arreglo asociativo es entonces:
void remove(int llave) {
EslabonM anterior= primero;
EslabonM proximo= primer.proximo;
while (proximo!=null && proximo.llave!=llave) {
anterior= proximo;
proximo= proximo.proximo;
}
if (proximo==null) // la llave no existe en el arreglo asociativo
return;
// la llave si existe, por lo que se elimina el eslabon
// referenciado por proximo
anterior.proximo= proximo.proximo;
}
Observe que construir un arreglo asociativo de n llaves toma tiempo O(n*n), lo que sabemos es muy ineficiente de acuerdo a lo estudiado con los algoritmos de ordenamiento.
En la próxima clase veremos una implementación eficiente de un arreglo asociativo que permite construir un arreglo con n asociaciones en tiempo O(n*log n) en el caso promedio. Esta implementación estará basada en un nueva estructura de datos: el árbol de búsqueda binaria.
Resumen
Todas las operaciones que hemos realizado con listas enlazadas se pueden resumir en los siguientes patrones de programación: