Computación I

Cálculo de Áreas

Objetivos: Resolver el problema de cálculo del área bajo la curva y utilizar subclases para poder formar una clase de biblioteca que realiza el cálculo.

Temas:

Cálculo de áreas.
Método de los trapecios.
Programación del método de los trapecios.
Cálculo del área de múltiples funciones en base a subclases.
Método de Simpson.

Cálculo de áreas

Uno de los problemas matamáticos más frecuentes es el cálculo del área que se forma al graficar una función. Por ejemplo, se necesita calcular el área A que aparece en la siguiente figura:

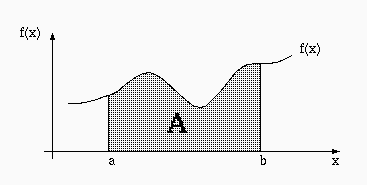
en donde la función f(x) y los valores a y b son conocidos.

En este tipo de problemas se pueden obtener dos tipos de soluciones:

Soluciones algebraicas: se obtiene una fórmula precisa y exacta para el área solicitada.
Soluciones numéricas: se calcula numéricamente una estimación del área.

Desde luego, la soluciones algebraicas son mejores que las numéricas, porque son exactas. Pero a veces, la complejidad de las funciones hace imposible (o difícil) obtener la solución algebraica, por lo que una solución numérica permite ahorrar tiempo.

Método de los trapecios

La estrategia más simple consiste en subdividir el intervalo pedido para el cálculo del área en n subintervalos de pequeño tamaño y aproximar el área como la suma de las área de los trapecios que se forman:

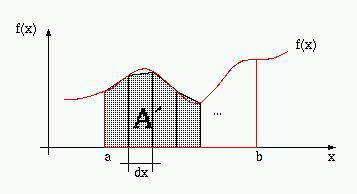
en donde delta=(a-b)/n. Si n es suficientemente grande (o equivalentemente delta es suficientemente pequeño), el área de los trapecios será aproximadamente el área pedida. El área de los trapecios se calcula de la siguiente forma:

Se determinan los puntos del eje x que delimitarán cada trapecio. Estos puntos son:

xi= a+delta*i, i= 0, 1, 2, ..., n
Se evalúa la función f en cada uno de los puntos xi:

yi= f(xi), i= 0, 1, 2, ..., n
Se calcula el área de cada trapecio como:

ai= (yi+y(i+1))*delta/2, i= 0, 1, 2, ..., n-1
Se suman las áreas de los trapecios.

Programación del método de los trapecios

Supongamos que la función eval evalúa la función f(x) (como se hizo cuando se calcularon la raíces de una función). Entonces la siguiente fórmula permite calcular el área de los trapecios:

area= delta*(f(a)/2+f(x1)+f(x2)+...+f(x(n-1))+f(b)/2)

Programa:

    double area(double a, double b, int n) {
      double delta= (b-a)/n;
      double sum= (eval(a)+eval(b))/2; // 1/2*(f(a)+f(b))
      double x= a;
      for (int i=1; i<n; i++) {        // + f(a+i*delta), con i=1 ... n-1
        x+= delta;
        sum+= eval(x);
      }
      return delta*sum;
    }
    double eval(double x) {
      ...
      return ...;
    }

Esta solución es análoga a la que se programó para buscar los ceros de una función. El problema de esta solución es que sucede cuando se requiere calcular la integral de varias funciones distintas. Hay que programar una función para calcular el área de cada función.

Cálculo del área de múltiples funciones en base a subclases

La idea consiste en crear objetos para evaluar las múltiples funciones. Cada uno de estos objetos poseerá un método eval para evaluar la función asignada. La definición del método se hará en una subclase de un clase base común a todas las funciones. Llamaremos a esta clase Funcion:

    class Funcion extends Program {
      double eval(double x) {
        return 0.0;
      }
      double area(double a, double b, int n) {
        // el mismo método de antes
        return ...;
      }
    }

Con esta clase ahora es posible calcular en un solo programa el área de sin(x), de exp(x) y de x^k:

    class FunSin extends Funcion {
      double eval(double x) {
        return sin(x);
      }
      // area se hereda
    }
    class FunExp extends Funcion {
      double eval(double x) {
        return exp(x);
      }
      // area se hereda
    }
    class FunXk extends Funcion {
      int k;
      FunXk(int k) {
        this.k= k;
      }
      double eval(double x) {
        return pow(x, k);
      }
      // area se hereda
    }
    ...
    void run() {
      println("area sin(x)= " + new FunSin().area(0.0, PI/2, 100));
      println("area exp(x)= " + new FunExp().area(0.0, 1.0, 100));
      println("area x^3= " + new FunXk(3).area(0.0, 1.0, 100));
    }

(Ver el programa completo en Trapecios.java.)

En la clase Funcion también se pueden incluir otros métodos para:

Graficar un intervalo de la función en una pizarra.
Buscar el mínimo en un intervalo de la función.
Buscar el máximo en un intervalo de la función.
Buscar una raiz de la función en un intervalo.
etc.

Método de Simpson

El método de los trapecios no es preciso en su resultado porque no es adecuado aproximar la curva por líneas rectas. Un método más preciso es el de Simpson que toma pares de subintervalos y aproxima la función en ese intervalo por un polinomio de grado 2 que pasa exactamente por los puntos que delimitan cada subintervalo.

Cada subintervalo entre xi y x(i+2), con i un entero par, se aproxima por un polinomio de la forma:

p(x)= ai*x²+bi*x+ci

en donde ai, bi y ci se calcula de tal forma que:

p(xi)=f(xi)
p(x(i+1))=f(x(i+1))
p(x(i+2))=f(x(i+2))

Al resolver el problema se llega a una formula bastante simple para el área:

area= delta/3*(f(a)+4*f(xi)+2*f(x(i+1))+4*f(x(i+2))+2*f(x(i+3))+...+4*f(x(n-1))+f(b))

Tarea:

Escriba el método simpson que calcula el área utilizando el método de simpson.

(Compare su solución con el programa Simpson.java.)