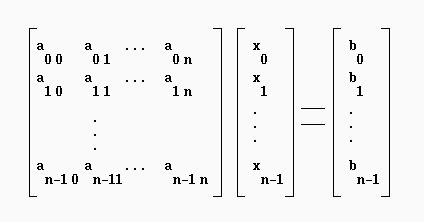
El mismo problema puede ser formulado matricialmente de la siguiente forma:

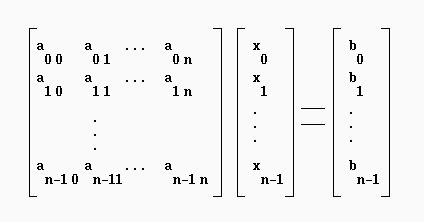
Para encontrar la solución es necesario triangularizar primero la matriz de modo de llegar a:

El programa que triangulariza la matriz es:

  void triangularizar(double[][] a, double[] b, int n) {
    for(int i=0; i<n; i++) {
      // *
      // dividir fila i por primero de fila i
      double prim= a[i][i];
      for (int j=i; j<n; j++)
        a[i][j] /= prim;
      b[i] /= prim;

      // file j = file j - fila i * primero de fila j
      for(int j= i+1; j<n; j++) {
        prim= a[j][i];
        for(int k= i; k<n; k++)
          a[j][k] -= a[i][k]*prim;
        b[j] -= b[i]*prim;
      }
    }
  }

    // buscar la fila en donde se encuentra el maximo:
    // filmax tq |a[filmax][i]|= max({|a[j][i]| con j= i ... n})
    int filmax=i;
    double max= abs(a[filmax][i]);
    for (int f=i+1; f<n; f++) // desde i porque entre 0 e i-1 son ceros
      if (abs(a[f][i])>max) {
        filmax= f;
        max= abs(a[f][i]);
      }
    // intercambiar la fila filmax con la fila i
    for (int c= i; c<n; c++) {
      double aux= a[i][c];
      a[i][c]= a[filmax][c];
      a[filmax][c]= aux;
    }
    // y el vector b tambien
    double aux= b[i];
    b[i]= b[filmax];
    b[filmax]= aux;

    void resolver(double a[][], double[] b, double[] x, int n) {
      triangularizar(a, b, n);

      // cálculo de los resultados
      for (int i= n-1; i>=0; i--) {
        double sum= 0.0;
        for (int j= i+1; j<n; j++)
          sum += x[j]*a[i][j];
        x[i]= (b[i]-sum)/a[i][i];
      }
    }