Arboles de Búsqueda Binaria

Objetivos: Mostrar como se implementa un arreglo asociativo usando árboles de búsqueda binaria.

Temas:

Definición de árboles de búsqueda binaria

Un árbol es una estructura de datos recursiva que se puede caracterizar en forma inductiva:


Un árbol binario es un árbol en el que de cada nodo cuelgan a los más dos árboles binarios.

Un árbol de búsqueda binaria (ABB) es un árbol binario que almacena en cada nodo una llave. El árbol de búsqueda binaria cumple las siguientes propiedades:


Implementación de un arreglo asociativo con un árbol de búsqueda binaria

Representamos el arreglo asociativo mediante un objeto que tiene una referencia de la raíz de un ABB:

    class Map extends Program {
      Nodo raiz= null;
      ... operaciones del arreglo asociativo ...
    }
Cuando el arreglo está vacío, la raíz es nula y representa entonces el árbol vacío. Cuando el arreglo tiene al menos una asociación, la raíz no es nula y referencia un objeto de la clase Nodo que se define como:

    class Nodo {
      int llave;
      String val;
      Nodo izq;
      Nodo der;
      Nodo(int llave, String val, Nodo izq, Nodo der) {
        this.llave= llave;
        this.val= val;
        this.izq= izq;
        this.der= der;
      }
    }
En donde izq referencia la raíz del ABB izquierdo, o nulo si el ABB vacío, y der referencia respectivamente el ABB derecho. Un nodo almacena una asociación (llave, val), al igual que en una lista enlazada un eslabón almacena un asociación del arreglo asociativo.

La siguiente figura muestra dos posibles representaciones de un arreglo asociativo con asociaciones {3->"hola", 5->"que", 10->"tal"}:


Búsqueda en un ABB

Para implementar la operación getString se utiliza un patrón de programación denominado búsqueda en ABBs. Esta búsqueda hace uso de un método recursivo que llamaremos buscar:

    String getString(int llave) {
      return buscar(llave, raiz);
    }

    String buscar(int llave, Nodo nodo) {
      if (nodo==null)
        fatalError("La llave "+llave+" no existe en el arreglo");
      else if (llave==nodo.llave)
        return nodo.val;
      else if (llave<nodo.llave)
        return buscar(llave, nodo.izq);
      else
        return buscar(llave, nodo.der);
      return null; // Solo para evitar el error en compilacion
    }
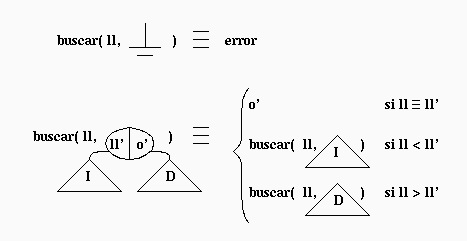
La siguiente figura muestra gráficamente el funcionamiento de este método:


Versión iterativa:

    String getString(int llave) {
      Nodo nodo= raiz;
      while (nodo!=null) {
        if (llave==nodo.llave)
          return nodo.val;
        if (llave<nodo.llave)
          nodo= nodo.izq;
        else
          nodo= nodo.der;
      }
      fatalError("La llave no existe en el arreglo");
      return null;
    }
Ejercicio: Implemente el método isMapped. Revise la clase anterior para obtener la especificación del comportamiento de este método.

Versión iterativa de la inserción en ABBs

Cuando se invoca la operación put, se presentan dos casos:

A continuación se presenta la implementación iterativa (es decir no recursiva) de put. Ésta resulta más simple conceptualmente que la implementación recursiva. Pero veremos que a la larga, la versión recursiva es un poco más breve que la iterativa.

    void put(int llave, String val) {
      if (raiz==null) {
        raiz= new Nodo(llave, val, null, null);
        return;
      }
      Nodo nodo= raiz;
      while (true) {
        if (nodo.llave==llave) {
          nodo.val= val;
          return;
        }
        if (nodo.llave>llave)
          if (nodo.izq!=null)
            nodo= nodo.izq;
          else {
            nodo.izq= new Nodo(llave, val, null, null);
            return;
          }
        else
          if (nodo.der!=null)
            nodo= nodo.der;
          else {
            nodo.der= new Nodo(llave, val, null, null);
            return;
          }
      }
    }
Esta solución no es elegante porque hay que diferenciar el caso en que el árbol está vacío (raiz==null), que el eslabón se agregue al lado izquierdo o que que se agregue al lado derecho. Sin embargo, esta solución es ligéramente más eficiente en un factor constante que la solución recursiva porque la iteración es más rápida que las llamadas recursivas.

Versión recursiva de la inserción en ABBs

Al igual que en el caso de la búsqueda de un nodo, se requiere introducir un nuevo método que será recursivo. Este método recibe como argumento la llave que se desea modificar, el nuevo valor asociado y la raíz del ABB en el que se debe realizar la modificación.

La clave para simplificar la implementación está en hacer que el método recursivo retorne una referencia del árbol modificado. En forma pictórica los distintos casos de modificación se explican en la siguiente figura:


Inserción en un ABB

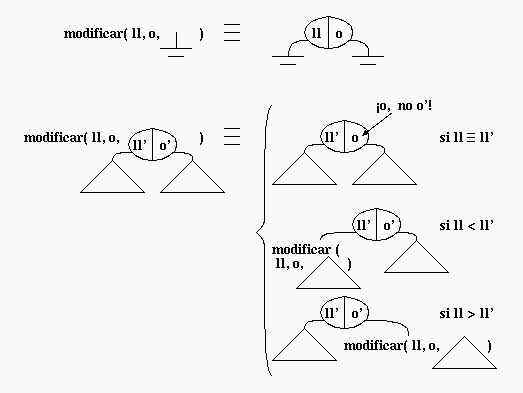
El código para implementar esta operación en Java es:

    void put(int llave, String val) {
      raiz= modificar(llave, val, raiz);
    }

    Nodo modificar(int llave, String val, Nodo nodo) {
      if (nodo==null)
        return new Nodo(llave, val, null, null);

      if (llave==nodo.llave)
        nodo.val= val;
      else if (llave<nodo.llave)
        nodo.izq= modificar(llave, val, nodo.izq);
      else
        nodo.der= modificar(llave, val, nodo.der);
      return nodo;
    }
Como podemos apreciar, la versión es un poco más breve que la versión iterativa. Sin embargo, ambas son igualmente eficientes.

Eliminación de nodos en ABBs

Para implementar el método remove se necesita usar el patrón de eliminación de nodos en ABBs. La siguiente figura explica en forma pictórica la lógica de este patrón:


Eliminación en un ABB

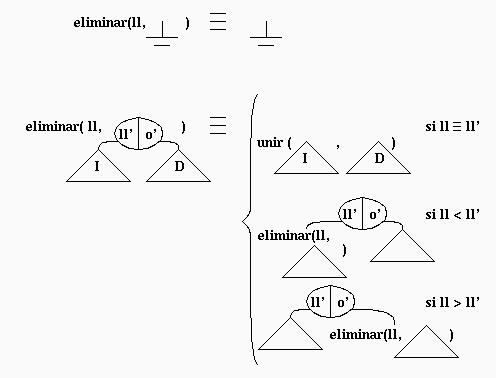
Para implementar esta operación se agrega el método recursivo eliminar. Este método recibe un ABB como parámetro y lo transforma de modo que ya no contenga la llave especificada. El método retorna el ABB modificado:

    void remove(int llave) {
      raiz= eliminar(llave, raiz);
    }

    Nodo eliminar(int llave, Nodo nodo) {
      if (nodo==null)
        return null;
      if (nodo.llave==llave)
        return unir(nodo.izq, nodo.der);

      if (llave<nodo.llave)
        nodo.izq= eliminar(llave, nodo.izq);
      else
        nodo.der= eliminar(llave, nodo.der);
      return nodo;
    }
El caso defícil se presenta cuando hay que eliminar un nodo, pero ese nodo tiene subárboles izquierdo y derecho al mismo tiempo. En este caso por lo tanto fabricamos un nuevo método que une dos ABBs (unir). El trabajo realizado por este método queda representado en la siguiente figura:


Unión de ABBs

El código de unir es:

    Nodo unir(Nodo izq, Nodo der) {
      if (izq==null)
        return der;
      if (der==null)
        return izq;
      Nodo centro= unir(izq.der, der.izq);
      izq.der= centro;
      der.izq= izq;
      return der;
    }
Análisis

Sea n el número de asociaciones que posee un arreglo asociativo. La siguiente tabla muestra el tiempo de ejecución en función de n para las operaciones típicas de un arreglo asociativo:

Operación Tiempo Tiempo
caso peor caso promedio
get O(n) O(log(n))
isMapped O(n) O(log(n))
put O(n) O(log(n))

Como vemos, el caso promedio es muy eficiente en comparación con la implementación que usa listas enlazadas.

Ejercicio 1: Implementación del método size

Implemente la operación size que calcula el número de asociaciones de un arreglo asociativo implementado mediante ABBs. Por ejemplo:

    Map m= new Map();
    println(m.size()); // 0
    m.put(3, "hola");
    m.put(5, "que");
    m.put(-1, "tal");
    println(m.size()); // 3

Ejercicio 2: Implementación del método findKey

Se desea desea agregar el método findKey a la clase Map. Este método recibe como parámetro un valor y debe entregar alguna llave a la cual se asocia ese objeto. El siguiente ejemplo muestra el uso de findKey:

    Map m= new Map();
    String s= "hola";
    m.put(10, s);
    m.put(5, "que");
    println(m.findKey(s)); // 10
Formalmente, findKey debe cumplir con la siguiente propiedad:

       Sea o un objeto cualquiera,
       si m.findKey(o)==ll entonces m.get(ll)==o
Observe que pueden existir varias llaves que se asocian con el mismo objeto o. En tal caso, m.findKey(o) entrega cualquiera de esas llaves. Si no existe ninguna llave, findKey termina la ejecución con un mensaje de error (invoca fatalError).

Implemente el método findKey para un arreglo asociativo implementado mediante ABBs.

Observación: Ud. debe buscar el objeto en todo el árbol. En este caso, el orden en que se encuentran las llaves en el ABB no sirve de nada. Por lo tanto su implementación tomará tiempo O(n).

Ejercicio 3: Implementación de arreglos con llaves de tipo string

Implemente la clase StringMap usando ABBs. Implemente las siguientes operaciones:

Ejemplo Significado Declaración
StringMap m= new StringMap(); Construye un arreglo asociativo con llaves de tipo string, inicialmente vacío StringMap()
m.put("juan", 1.7); Asocia el string "juan" con el real 1.7 void put(String ll, double v)
double v= m.getDouble("juan"); entrega el real asociado a la llave "juan". Si la llave no posee valor asociado se produce un error. double getDouble(String ll)

Ejercicio 4: Inserción en la raiz de ABBs

En la implementación hecha para put, el eslabón que contiene la llave queda en su posición original (cuando la llave existía) o en una hoja del árbol (cuando la llave no existía). Implemente una versión de put en donde la llave que se reasocia con un nuevo objeto siempre quede en la raíz del ABB.

Indicaciones: Suponga que el método recursivo que inserta la llave en la raíz del ABB se llama insertar. El caso simple es cuando la llave ya se encuentra en la raíz o el ABB está vacío. Analícelo. Cuando no se cumple ninguna de estas condiciones, sin pérdida de generalidad podemos suponer que la llave que se reasocia con un nuevo valor es menor que la llave almacenada en la raíz del ABB. La siguiente figura muestra cómo debe calcular el nuevo árbol en el caso en que la llave que se desea agregar es menor que la llave que se encuentra almacenada en la raíz del ABB (ll<ll'):


Inserción en la raíz de un ABB
(caso ll<ll')

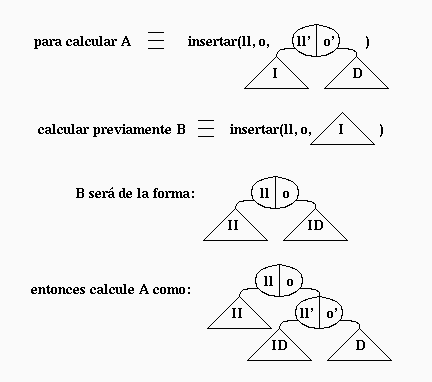
El resultado del método insertar será entonces el árbol A. Haga las figuras para los casos en que ll==ll' y ll>ll'. Finalmente programe los métodos put e insertar.

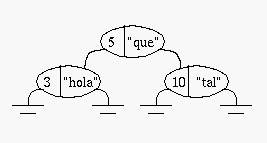
Ejercicio 5: Póngale nombre a la clase

Suponga que se tiene un arreglo asociativo m representado mediante el siguiente árbol:

A la clase Map se a agregado el siguiente método incógnito que retorna una instancia de una clase también incógnita, implementados mediante el siguiente código:

    class Map {
      Nodo raiz= null;
      ...
      Incognita incognito() {
        return new Incognita(raiz);
      }
    }

    class Incognita {
      PilaNodos pila= new PilaNodos();
      // Una pila de nodos

      Llaves(Nodo raiz) {
        Nodo nodo= raiz;
        while (nodo!=null) {
          pila.put(nodo);
          nodo= nodo.izq;
        }
      }

      // Tan pocas lineas y tan dificil de entender!
      int incognito2() {
        Nodo nodo= pila.getNodo();
        int res= nodo.llave;
        nodo= nodo.der;
        while (nodo!=null) {
          pila.put(nodo);
          nodo= nodo.izq;
        }
        return res;
      }

      boolean incognito3() { return !pila.isEmpty(); }
    }
Obs: La clase PilaNodos opera de la forma usual con las operaciones put, getNodo y isEmpty.

Ejecute paso a paso la siguientes invocaciones de método e indique el resultado de cada println:

    Incognita ign= m.incognito();
    println(ign.incognito2());
    println(ign.incognito2());
    println(m.incognito3());
    println(ign.incognito2());
    println(m.incognito3());
Revise los métodos de la clase StringMap descrita en el capítulo de TDAs. Póngale nombre a la clase y a los métodos incógnitos.