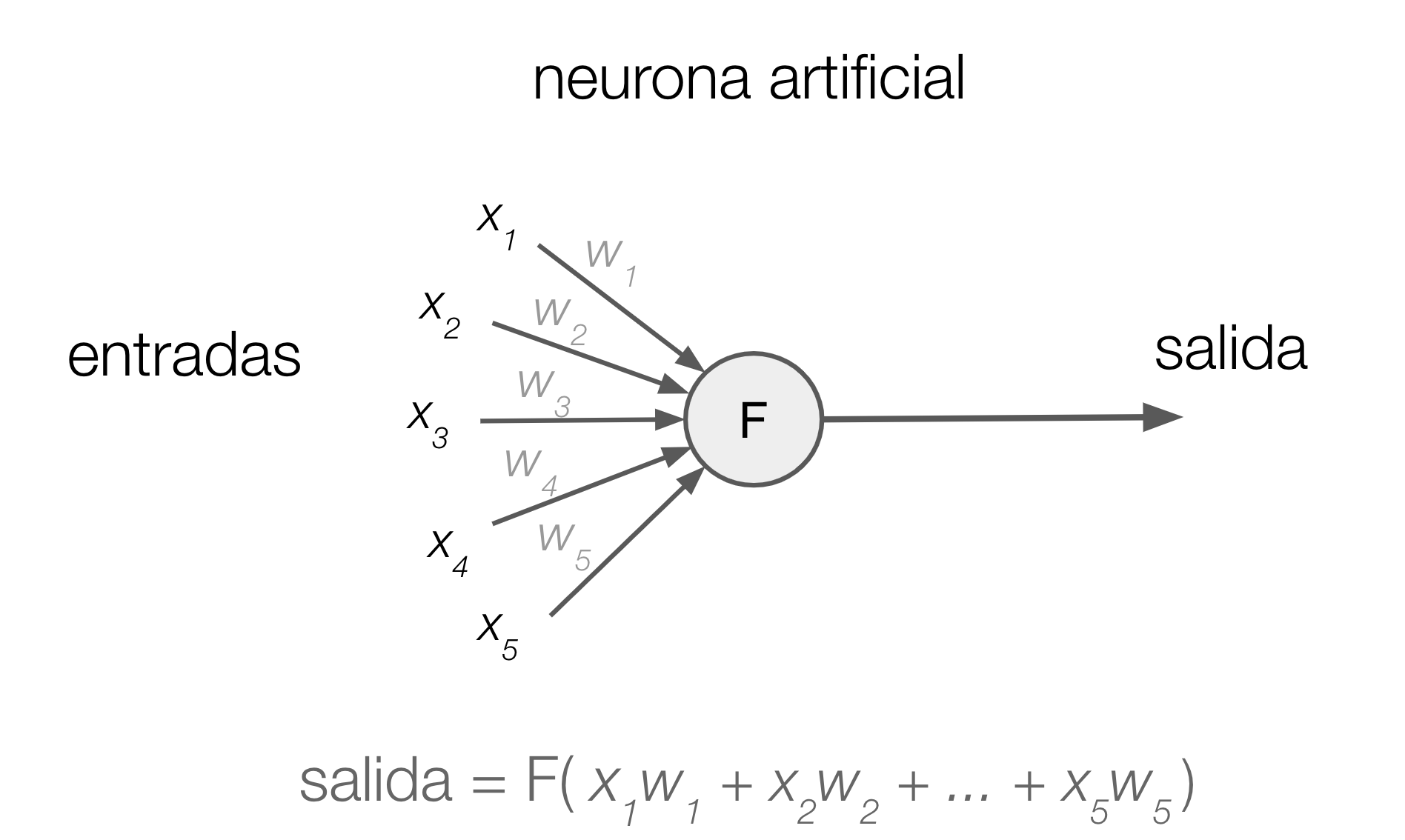
Figura 1: Neurona artificial con 5 entradas
Cada conexión está asociada a un número real llamado peso de la conexión o parámetro. Dadas entradas x1, x2, …, xn, una neurona artificial con pesos w1, w2, …, wn y función de activación F, entrega como salida
F( x1w1 + x2w2 + … + xnwn )
Es decir, la salida es el resultado de aplicar la función de activación a la suma de cada una de las entradas multiplicada por el peso de la conexión correspondiente. Haciendo el símil con una neurona biológica, las entradas representan los estímulos que recibe la neurona, los pesos representan a las dendritas y la función de activación al umbral de excitación de la neurona. Varias neuronas artificiales se pueden conectar para formar redes de neuronas (Figura 2). Típicamente las neuronas se conectan en capas de manera que las salidas de las neuronas de una capa son las entradas de las neuronas de la capa siguiente. Una red neuronal profunda es una que tiene varias de estas capas.
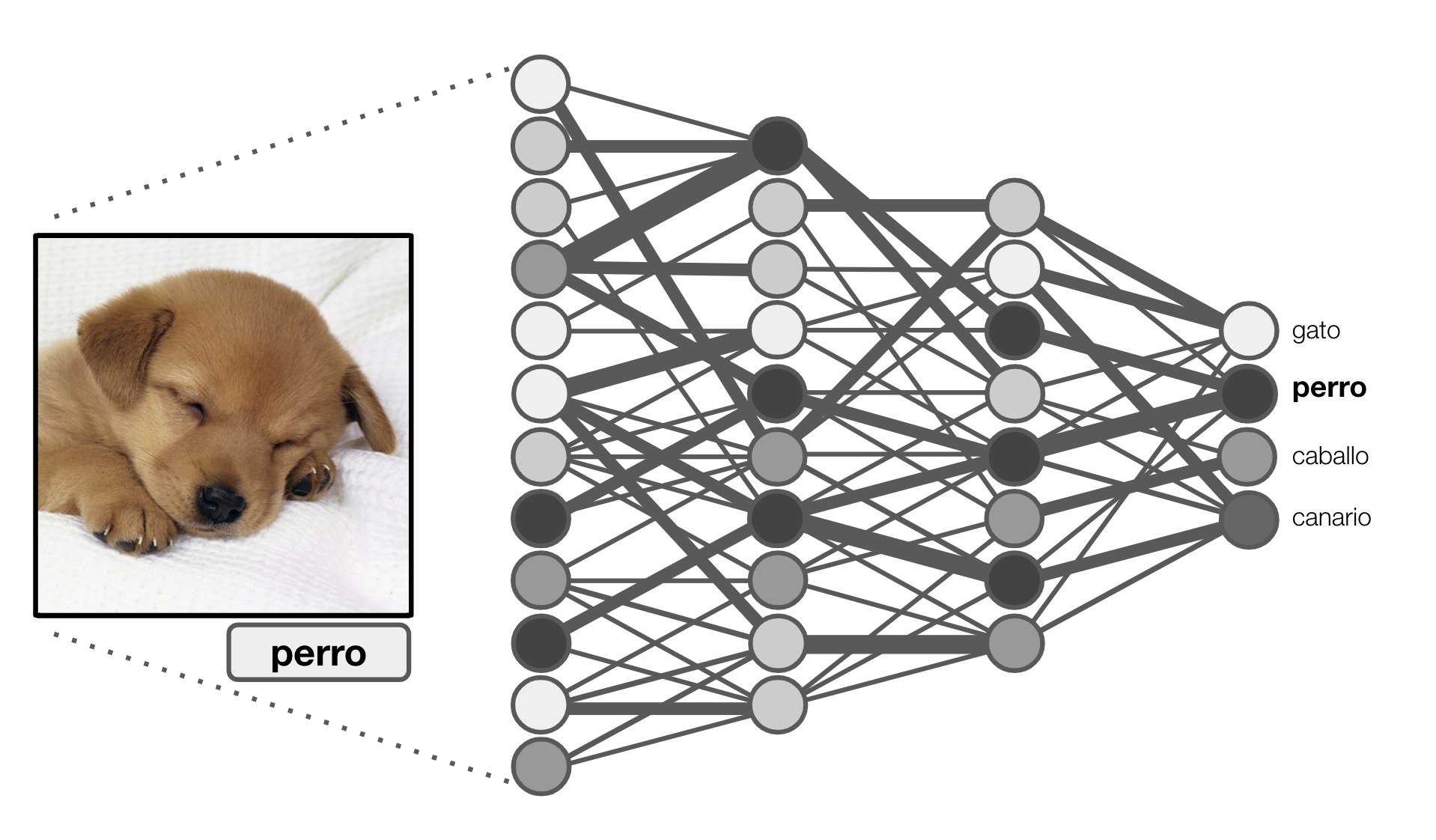
Figura 2: Red neuronal artificial de varias capas.
Dado un dato de entrada, por ejemplo una imagen, la red computa por capas los valores de salida de cada neurona. Los valores de la capa final se interpretan dependiendo de cada aplicación. La red de la Figura 2 es una hipotética red para clasificar imágenes en 4 clases. El ancho de cada conexión representa la magnitud de los pesos asociados, y el color de cada neurona representa la magnitud de su valor de salida cuando procesa el ejemplo de la figura. En la última capa la clase decidida por la red es la que corresponde a la neurona de valor más alto (en la Figura 2, la salida es “perro”). La salida que produce una red neuronal depende de los valores de entrada y de la magnitud de los pesos de cada una de las conexiones. Por lo tanto, si cambiamos los pesos de las conexiones cambiará también el funcionamiento de la red. Dado un conjunto de datos, podemos ir cambiando los pesos de la red de manera de adaptarla para que clasifique los datos tan bien como sea posible. Este proceso se llama entrenamiento.
Hinton y el algoritmo de propagación hacia atrás
En el artículo “Learning Internal Representations by Error Propagation” [RHW86a], en conjunto con D. Rumelhart y R. Williams, Hinton utilizó por primera vez la versión moderna del algoritmo de propagación de errores hacia atrás para entrenar una red neuronal artificial. Este algoritmo, conocido hoy como backpropagation, permite computar eficientemente la incidencia que tiene cada conexión de la red en el error total que la red comete cuando clasifica ejemplos. Usando una elegante combinación entre cálculo diferencial, la regla de la cadena y programación dinámica, backpropagation permite determinar cuánto se debe modificar cada conexión para hacer a la red más efectiva. Desde el artículo de Hinton y hasta la fecha, backpropagation es el estándar para entrenar redes neuronales. Pero en esta investigación Hinton fue más allá; mostró cómo una red neuronal entrenada con backpropagation podía descubrir representaciones internas de los datos de entrada que le permitían resolver problemas que hasta ese momento se creían imposibles de resolver con estas redes [RHW86a,RHW86b].
A pesar de lo promisorio del algoritmo, su aplicación a gran escala no fue inmediata principalmente por la falta de poder computacional y la escasez de datos de entrenamiento. No fue sino hasta el año 2012 cuando Hinton y un grupo de estudiantes [KSH12] usó backpropagation más un conjunto de ingeniosas optimizaciones para ganar ImageNet, uno de los más importantes desafíos de clasificación de imágenes. Las redes neuronales superaron por amplio margen a los modelos competidores, cambiando de manera radical el área de visión computacional. El triunfo en ImageNet es considerado por muchos como el hito que cambió la percepción del mundo científico acerca de las redes neuronales artificiales.
LeCun y las redes convolucionales
Lo esencial de la red usada por Hinton y sus estudiantes para ganar ImageNet había sido propuesto más de 20 años atrás, en 1989, por Yann LeCun. En el artículo “Generalization and Network Design Strategies” [LeCun89] LeCun se basó en la siguiente observación: las características distintivas de un objeto pueden aparecer en cualquier lugar de una imagen que contenga a ese objeto. Pensemos por ejemplo en la rueda de una bicicleta; ésta puede aparecer tanto en el extremo izquierdo como en el centro de una imágen, sin dejar de ser la rueda de una bicicleta. LeCun ideó una red neuronal que para procesar imágenes consideraba pequeñas ventanas, también llamadas filtros, que podrían usarse para encontrar características específicas dentro de una imagen sin importar dónde éstas aparecieran. Para implementar los filtros, las conexiones de distintas neuronas estaban obligadas a compartir la misma magnitud modelando de esta manera la capacidad de reconocer una misma característica en distintos lugares de la imágen. Si bien la idea de usar filtros para procesar imágenes no era nueva, el cambio que introdujo LeCun fue dejar que la red neuronal aprendiera los filtros necesarios usando backpropagation y datos de entrenamiento, en vez de ser diseñados a mano. La red de LeCun, que hoy conocemos como red convolucional, tenía otra característica importante: al obligar que conexiones de distintas neuronas tuvieran la misma magnitud, la cantidad total de pesos distintos en la red se disminuye de manera sustancial lo que facilitaba considerablemente el entrenamiento.
Las redes de LeCun tuvieron un uso práctico casi inmediato. A finales de los 90’s cerca del 20% de todos los cheques de Estados Unidos eran procesados automáticamente por una red neuronal convolucional. Sin embargo su propuesta no tuvo eco en la comunidad científica que seguía prefiriendo métodos alternativos para procesar imágenes, en parte por la falta del software necesario, y en parte por lo difícil de conseguir datos para entrenamiento. LeCun hizo esfuerzos para mejorar ambos aspectos. Junto a L. Bottou, escribió el primer software para facilitar la implementación de redes neuronales [BL88]. El software llamado SN tenía una sintaxis similar a LISP y corría sobre AmigaOS. También recopiló el conjunto de datos MNIST [MNIST] que contiene 60.000 imágenes de dígitos escritos a mano y que sigue siendo utilizado como conjunto de datos de entrenamiento y prueba de redes neuronales hasta el día de hoy.
Bengio y el procesamiento y creación de datos complejos
Tanto las redes neuronales tradicionales como las convolucionales tienen la desventaja de que su entrada debe ser de tamaño fijo. Durante los años 90’s Yoshua Bengio hizo aportes cruciales en la teoría y la práctica de redes neuronales recurrentes que son capaces de procesar secuencias de largo arbitrario con una cantidad fija de conexiones. El trabajo de Bengio [BSF94], y otros pioneros del área como J. Schmidhuber [HS97], mostró que las redes neuronales podían utilizarse para procesar series de tiempo, clasificar texto y reconocer voz.
Bengio ha estado también involucrado en tres de los avances más importantes en redes neuronales del último tiempo: la simplificación de las funciones de activación [GBB11], el mecanismo de atención [BChB15], y las redes generativas adversarias [G14]. El primer trabajo introdujo la unidad lineal rectificada (ReLU) que simplificó radicalmente el proceso de entrenamiento. ReLU es hoy la función de activación utilizada por defecto en la mayoría de las redes neuronales. El segundo trabajo implicó una contribución fundamental en procesamiento de lenguaje natural que ha permitido el florecimiento de, por ejemplo, sistemas de traducción automática de alta precisión. El tercero es considerado por muchos como la idea más importante acerca de redes neuronales de los últimos 20 años. Es una técnica, desarrollada por I. Goodfellow, Bengio y otros colaboradores, en la que dos redes se entrenan simultáneamente en una competencia. Por ejemplo, una red A se entrena para producir imágenes de personas, mientras otra red B se entrena para identificar si una imagen de una persona es real o si fue producida por A. El objetivo de A es engañar a B, mientras que el objetivo de B es no ser engañado por A. El entrenamiento conjunto le permite a la red A generar objetos nuevos de increíble parecido a la realidad (Figura 3).
Figura 3: Imágenes de caras generadas por una red generativa adversaria
Epílogo: La revolución actual y futura
Hace 10 años, muy pocos se hubieran imaginado que el premio Turing sería entregado a científicos trabajando en redes neuronales artificiales. Hoy usamos redes neuronales sin darnos cuenta en muchas tareas, como cuando usamos un traductor automático o mejoramos la calidad de una foto tomada con poca luz. También se usan en el área de la salud, planificación urbana, conducción asistida de automóviles e incluso composición musical. Las aplicaciones de hoy se deben en gran parte a tres científicos que visualizaron que era solo cuestión de tiempo para que la revolución ocurriera. Visualizaron que con el software y hardware necesarios, sólo habría que esperar a que los datos estuvieran disponibles para lograr la eficacia requerida para superar a la mayoría de los métodos tradicionales.
Los tres científicos advierten que el siguiente paso en la revolución de la inteligencia artificial vendrá de ideas radicalmente distintas a las que hoy se utilizan. LeCun, en su ya famosa frase “la revolución de las máquinas no será supervisada”, nos invita a diseñar sistemas que puedan aprender sin supervisión, a diferencia de la tendencia predominante de aprendizaje desde datos etiquetados. Por su parte Bengio ha sido uno de los impulsores de la combinación entre redes neuronales y razonamiento lógico simbólico, dos áreas que históricamente se han considerado como antagonistas. Los tres observan que una característica de la que hoy carecen las redes neuronales es de la capacidad para construir modelos del mundo, algo como tener sentido común. Por ejemplo, desde imágenes las redes no son capaces de aprender que un gato no puede volar, o que la gravedad siempre apunta hacia abajo. Para construir sistemas con inteligencia general éstos deben ser capaces de entender el mundo más allá de lo que se necesita para resolver una tarea específica.
Hinton nos deja con el siguiente mensaje: “si tienes una idea y el convencimiento absoluto de que la idea está correcta, no permitas que la gente te convenza de que es una estupidez, simplemente ignóralos”. A la obstinación de Hinton, Bengio y LeCun, junto a sus colaboradores y otros pioneros del área, le debemos la actual revolución en inteligencia artificial. Tendremos que esperar por nuevos obstinados y obstinadas que guíen la próxima revolución.
Jorge Pérez
Profesor Asociado, DCC-UChile
Investigador Asociado, IMFD
Bibliografía
[MP43] W. McCulloch and W. Pitts. A logical calculus of ideas immanent in nervous activity. Bulletin of Mathematical Biophysics, 5:127–147, 1943.
[K56] S. C. Kleene. Representation of events in nerve nets and finite automata. In Automata Studies, pp. 3-41. Princeton University Press, 1956.
[R58] F. Rosenblatt. The Perceptron: A Probabilistic Model for Information Storage and Organization in the Brain, Psychological Review, vol. 65, 6:386–408, 1958.
[NYT58] Electronic Brain Teaches Itself. The New York Times, July 13, Page 9, 1958.
[MP69] M. Minsky, S. A. Papert. Perceptrons, MIT press, 1969
[ACM19] ACM Announces 2018 Turing Award Recipients, March 27, 2019, https://awards.acm.org/about/2018-turing
[RHW86a] D. E. Rumelhart, G. E. Hinton, R. J. Williams. Learning Internal Representations by Error Propagation, Parallel Distributed Processing: Explorations in the Microstructure of Cognition. Vol. 1: Foundations, 318–362, 1986
[RHW86b] D. E. Rumelhart, G. E. Hinton, R. J. Williams. Learning representations by back-propagating errors, Nature, 323:533–536, 1986.
[KSH12] A. Krizhevsky, I. Sutskever, G. E. Hinton. ImageNet classification with deep convolutional neural networks, Advances in Neural Information Processing Systems, 1106-1114, 2012
[LeCun89] Y. LeCun. Generalization and Network Design Strategies. Tech Report, U. of Toronto, 1989
[BL88] L. Bottou, Y. LeCun. SN: A simulator for connectionist models. NeuroNimes, 1988
[MNIST] Y. LeCun, C. Cortes, C. Burges. MNIST handwritten digit database, http://yann.lecun.com/exdb/mnist/
[BSF94] Y. Bengio, P. Simard, P. Frasconi. Learning long-term dependencies with gradient descent is difficult, IEEE transactions on neural networks 5 (2), 157-166
[HS97] S. Hochreiter, J. Schmidhuber. Long Short-Term Memory, Neural computation 9(8), 1735-1780, 1997
[GBB11] X. Glorot, A. Bordes, Y. Bengio. Deep sparse rectifier neural networks. AISTATS 2011.
[BChB15] D. Bahdanau, K. Cho, Y. Bengio. Neural Machine Translation by Jointly Learning to Align and Translate. International Conference on Learning Representations, 2015.
[G14] I. Goodfellow et. al. Generative Adversarial Nets, Advances in Neural Information Processing Systems, 2672-2680, 2014