Compresión de datos

En esta sección veremos la aplicación de la teoría de árboles a la compresión de datos. Por compresión de datos entendemos cualquier algoritmo que reciba una cadena de datos de entrada y que sea capaz de generar una cadena de datos de salida cuya representación ocupa menos espacio de almacenamiento, y que permite -mediante un algoritmo de descompresión- recuperar total o parcialmente el mensaje recibido inicialmente. A nosotros nos interesa particularmente los algoritmos de compresión sin pérdida, es decir, aquellos algoritmos que permiten recuperar completamente la cadena de datos inicial.

Codificación de mensajes

Supongamos que estamos codificando mensajes en binario con un alfabeto de tamaño $n$. Para esto se necesitan $\left\lceil log_{2}(n)\right\rceil$ bits por símbolo, si todos los códigos son de la misma longitud.

Ejemplo: para el alfabeto A,$...$,Z de 26 letras se necesitan códigos de $\left\lceil log_{2}(26)\right\rceil =5$ bits

Problema: Es posible disminuir el número promedio de bits por símbolo?

Solución: Asignar códigos más cortos a los símbolos más frecuentes.

Un ejemplo claro de aplicación de este principio es el código morse:

A	. -
B	- . . .
$\vdots$
E	.
$\vdots$
Z	- - . .

Se puede representar mediante un arbol binario:

Podemos ver en el árbol que letras de mayor probabilidad de aparición (en idioma inglés) están más cerca de la raíz, y por lo tanto tienen una codificación más corta que letras de baja frecuencia.

Problema: este código no es auto-delimitante

Por ejemplo, SOS y IAMS tienen la misma codificación

Para eliminar estas ambigüedades, en morse se usa un tercer delimitador (espacio) para separar el código de cada letra. Se debe tener en cuenta que este problema se produce sólo cuando el código es de largo variable (como en morse), pues en otros códigos de largo fijo (por ejemplo el código ASCII, donde cada caracter se representa por 8 bits) es directo determinar cuales elementos componen cada caracter.

La condición que debe cumplir una codificación para no presentar ambigüedades, es que la codificación de ningun caracter sea prefijo de otra. Esto nos lleva a definir árboles que sólo tienen información en las hojas, como por ejemplo:

Como nuestro objetivo es obtener la secuencia codificada más corta posible, entonces tenemos que encontrar la codificación que en promedio use el menor largo promedio del código de cada letra.

Problema: Dado un alfabeto ${a_{1},\ldots ,a_{n}}$ tal que la probabilidad de que la letra $a_{i}$ aparezca en un mensaje es $p_{i}$, encontrar un código libre de prefijos que minimice el largo promedio del código de una letra.

Supongamos que a la letra $a_{i}$ se le asigna una codificación de largo $t_{i}$, entonces el largo esperado es:

$$\sum _{i}p_{i}t_{i}$$

es decir, el promedio ponderado de todas las letras por su probabilidad de aparición.

Ejemplo:

	probabilidad	código
A	0.30	00
B	0.25	10
C	0.08	0110
D	0.20	11
E	0.05	0111
F	0.12	010

$$\begin{eqnarray*} Costo\: esperado & = & 2(0.30+0.25+0.20)+3(0.12)+4(0.08+0.05)\\ & = & 2.075+0.36+0.52\\ & = & 2.38\, bits\, por\, simbolo \end{eqnarray*}$$

Entropía de Shannon

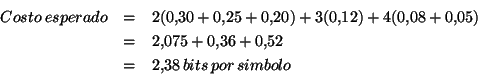
Shannon define la entropía del alfabeto como:

$$-\sum _{i}p_{i}\log _{2}(p_{i})$$

El teorema de Shannon dice que el número promedio de bits esperable para un conjunto de letras y probabilidades dadas se aproxima a la entropía del alfabeto. Podemos comprobar esto en nuestro ejemplo anterior donde la entropia de Shannon es:

$$\begin{eqnarray*} Entropia & = & -(0.30\log _{\textrm{2}}(0.30)+0.25\log _{\text... ...& = & 0.521+0.5+0.2915+0.4643+0.2160+0.3670\\ & \approx & 2.36 \end{eqnarray*}$$

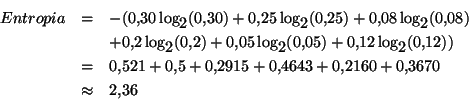
que es bastante cercano al costo esperado de 2.38 que calculamos anteriormente.

A continuación describiremos algoritmos que nos permitan encontrar representaciones que minimicen el costo total.

Algoritmo de Huffman

El algoritmo de Huffman permite construir un código libre de prefijos de costo esperado mínimo.

Inicialmente, comenzamos con $n$ hojas desconectadas, cada una rotulada con una letra del alfabeto y con una probabilidad (ponderacion o peso).

Consideremos este conjunto de hojas como un bosque. El algoritmo es:

while(nro de árboles del bosque > 1){

  - Encontrar los 2 árboles de peso mínimo y  
    unirlos con una nueva raíz que se crea para esto.

  - Arbitrariamente, rotulamos las dos 

    líneas como ´ 0´ y ´ 1´

  - Darle a la nueva raíz un peso que es  
    la suma de los pesos de sus subárboles.

  }

Ejemplo:

Si tenemos que las probabilidades de las letras en un mensaje son:

Entonces la construcción del árbol de Huffman es (los números en negrita indican los árboles con menor peso):

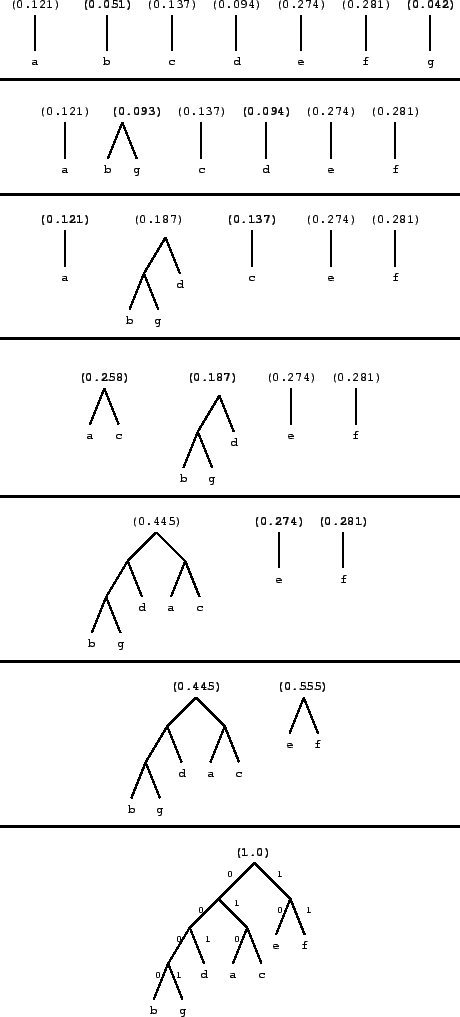
Se puede ver que el costo esperado es de 2,53 bits por letra, mientras que una codificación de largo fijo (igual número de bits para cada símbolo) entrega un costo de 3 bits/letra.

El algoritmo de codificación de Huffman se basa en dos supuestos que le restan eficiencia:

1. supone que los caracteres son generados por una fuente aleatoria independiente, lo que en la práctica no es cierto. Por ejemplo, la probabilidad de encontrar una vocal después de una consonante es mucho mayor que la de encontrarla después de una vocal; después de una q es muy probable encontrar una u, etc
2. Debido a que la codificación se hace caracter a caracter, se pierde eficiencia al no considerar las secuencias de caracteres más probables que otras.

Lempel Ziv

Una codificación que toma en cuenta los problemas de los supuestos enunciados anteriormente para la codificación de Huffman sería una donde no solo se consideraran caracteres uno a uno, sino que donde además se consideraran aquellas secuencias de alta probabilidad en el texto. Por ejemplo, en el texto:

aaabbaabaa

Obtendríamos un mayor grado de eficiencia si además de considerar caracteres como a y b, también considerásemos la secuencia aa al momento de codificar.

Una generalización de esta idea es el algoritmo de Lempel-Ziv. Este algoritmo consiste en separar la secuencia de caracteres de entrada en bloques o secuencias de caracteres de distintos largos, manteniendo una diccionario de bloques ya vistos. Aplicando el algoritmo de Huffman para estos bloques y sus probabilidades, se puede sacar provecho de las secuencias que se repitan con más probabilidad en el texto. El algoritmo de codificación es el siguiente:

1.- Inicializar el diccionario con todos  
    los bloques de largo 1

2.- Seleccionar el prefijo más largo del  
    mensaje que calce con alguna secuencia W  
    del diccionario y eliminar W del mensaje

3.- Codificar W con su índice en el diccionario

4.- Agregar W seguido del primer símbolo del  
    próximo bloque al diccionario.

5.- Repetir desde el paso 2.

Ejemplo:

Si el mensaje es

$abbaabbaababbaaaabaabba$

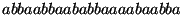
la codificación y los bloques agregados al diccionario serían (donde los bloques reconocidos son mostrados entre paréntesis y la secuencia agregada al diccionario en cada etapa es mostrada como un subíndice):

$$(a)_{ab}(b)_{bb}(b)_{ba}(a)_{aa}(ab)_{abb}(ba)_{baa}(ab)_{aba}(abb)_{abba}(aa)_{aaa}(aa)_{aab}(baa)_{baab}(bb)_{bba}(a)$$

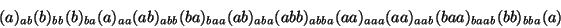
Teóricamente, el diccionario puede crecer indefinidamente, pero en la práctica se opta por tener un diccionario de tamaño limitado. Cuando se llega al límite del diccionario, no se agregan más bloques.

Lempel-Ziv es una de las alternativas a Huffman. Existen varias otras derivadas de estas dos primeras, como LZW (Lempel-Ziv-Welch), que es usado en programas de compresión como el compress de UNIX.