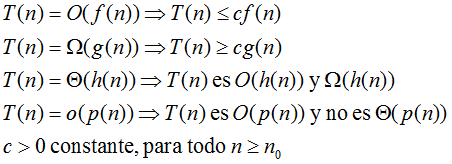
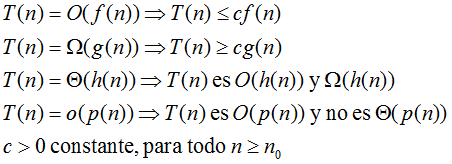
Al programar en forma recursiva, buscamos dentro de un problema otro subproblema que posea su misma estructura.
Ejemplo: Calcular xn.
// Version 1
public static float elevar( float x, int n )
{
if( n==0 )
return 1;
else
return x * elevar(x, n-1);
}
// Version 2
public static float elevar( float x, int n )
{
if( n==0 )
return 1;
else if( n es impar )
return x * elevar( x, n-1 );
else
return elevar( x*x, n/2 );
}
Ejemplo: Torres de Hanoi.
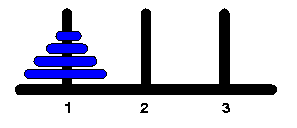
public class TorresDeHanoi{
static void Hanoi( int n, int a, int b, int c ){
if (n>0){
Hanoi( n-1, a, c, b );
System.out.println( a + " --> " + c );
Hanoi( n-1, b, a, c );
}
}
public static void main(String[] args){
Hanoi(Integer.parseInt(args[0]), 1, 2, 3);
}
}
Esta técnica de diseño de algoritmos consiste en resolver un problema por prueba y error. Se basa en generar todas las posibles soluciones al problema utilizando recursión, probando cada una de ellas hasta encontrar aquella que lo resuelve. Por esto mismo, el tiempo requerido para solucionar el problema puede ser muy alto (por ejemplo, exponencial en el tamaño de la entrada).
Ejemplo: El laberinto.
Se tiene una matriz de caracteres de dimensiones N = filas x columnas, que representa un laberinto. Se comienza desde una posición (i,j) dada y el objetivo es encontrar la salida, permitiendo sólo desplazamientos horizontales y verticales. La codificación del laberinto es la siguiente:
* * * * * * * * * * * * * * * * * & * * * * * * * * * * * * * * * * * * * * * * * * * *
El método a implementar es boolean salida(char[][] x, int i, int j), que retorna true si desde la posición i,j se puede encontrar una salida. Este problema se puede resolver utilizando backtracking de la siguiente forma:
Una primera versión de la función en Java que instancia este algoritmo podría ser la siguiente (supuesto: todo el borde del laberinto esta rodeado por paredes, excepto en la(s) salida(s)):
public static salida1(char[][] x, i, j)
{
if (x[i][j] == '&') return true;
if (x[i][j] == '*') return false;
if (salida1(x, i+1, j)) return true;
if (salida1(x, i-1, j )) return true;
if (salida1(x, i, j+1)) return true;
if (salida1(x, i, j-1,)) return true;
return false;
}
Esta implementación tiene el problema que puede generar un número infinito de llamados recursivos. Por ejemplo, si se invoca a salida1(x, a, b) y es una celda de pasillo, ésta invocará recursivamente a salida1(x, a+1, b). Si la celda (a+1,b) es una celda de pasillo, puede potencialmente invocar a salida1(x, a+1-1, b), generandose así un ciclo infinito de llamados recursivos. Para evitar este problema, se puede ir marcando (por ejemplo, con el carácter '+') las celdas por donde el algoritmo ya pasó, evitando caer en el ciclo infinito:
public static boolean salida(char[][] x, i, j) // correcto
{
if (x[i][j] == '&') return true;
if (x[i][j] == '*' || x[i][j] == '+') return false;
x[i][j] = '+';
if (salida(x, i+1, j)) return true;
if (salida(x, i-1, j)) return true;
if (salida(x, i, j+1)) return true;
if (salida(x, i, j-1)) return true;
return false;
}
Propuesto: Modifique la implementación de la función salida para que retorne un String que contenga la secuencia de celdas (i,j) por donde hay que pasar para llegar a la salida del laberinto. El nuevo encabezado de la función es public static String salida(char[][] x, int i, int j). Finalmente, implemente la función salida de modo que retorne la secuencia de celdas más corta para llegar a la salida.
Este es un método de diseño de algoritmos que se basa en subdividir el problema en sub-problemas, resolverlos recursivamente, y luego combinar las soluciones de los sub-problemas para construir la solución del problema original.
Ejemplo: Multiplicación de Polinomios.
Supongamos que tenemos dos polinomios con n coeficientes, o sea, de grado n-1:
A(x) = a0+a1*x+ ... +an-1*xn-1 B(x) = b0+b1*x+ ... +bn-1*xn-1
representados por arreglos a[0], ..., a[n-1] y b[0], ..., b[n-1]. Queremos calcular los coeficientes del polinomio C(x) tal que C(x) = A(x)*B(x).
Un algoritmo simple para calcular esto es:
// Multiplicación de polinomios
for( k=0; k<=2*n-2; ++k )
c[k] = 0;
for( i=0; i<n; ++i)
for( j=0; j<n; ++j)
c[i+j] += a[i]*b[j];
Evidentemente, este algoritmo requiere tiempo O(n2). ¿Se puede hacer más rápido?
Supongamos que n es par, y dividamos los polinomios en dos partes. Por ejemplo, si
A(x) = 2 + 3*x - 6*x2 + x3
entonces se puede reescribir como
A(x) = (2+3*x) + (-6+x)*x2
y en general
A(x) = A'(x) + A"(x) * xn/2 B(x) = B'(x) + B"(x) * xn/2
Entonces
C = (A' + A"*xn/2) * (B' + B"*xn/2) = A'*B' + (A'*B" + A"*B') * xn/2 + A"*B" * xn
Esto se puede implementar con 4 multiplicaciones recursivas, cada una involucrando polinomios de la mitad del tamaño que el polinomio original. Si llamamos T(n) al número total de operaciones, éste obedece la ecuación de recurrencia
T(n) = 4*T(n/2) + K*n
donde K es alguna constante cuyo valor exacto no es importante.
TeoremaLas ecuaciones de la forma
T(n) = p*T(n/q) + K*ntienen solución
T(n) = O(nlogq p) (p>q) T(n) = O(n) (p<q) T(n) = O(n log n) (p=q)(Nota: este Teorema, conocido como el Teorema Maestro, será demostrado más adelante.)
Por lo tanto la solución del problema planteado (p=4, q=2) es
T(n) = O(nlog2 4) = O(n2)
lo cual no mejora al algoritmo visto inicialmente.
Pero... hay una forma más eficiente de calcular C(x). Si calculamos:
D = (A'+A") * (B'+B") E = A'*B' F = A"*B"
entonces
C = E + (D-E-F)*xn/2 + F*xn
Lo cual utiliza sólo 3 multiplicaciones recursivas, en lugar de 4. Esto implica que
T(n) = O(nlog2 3) = O(n1.59)
A veces la simple recursividad no es eficiente.
Ejemplo: Números de Fibonacci.
Los números de Fibonacci se definen mediante la recurrencia
fn = fn-1+fn-2 (n>=2) f0 = 0 f1 = 1
cuyos primeros valores son
n 0 1 2 3 4 5 6 7 8 9 10 11 . . . fn 0 1 1 2 3 5 8 13 21 34 55 89 . . .
Se puede demostrar que los números de Fibonacci crecen exponencialmente, como una función O(øn) donde ø=1.618....
El problema que se desea resolver es calcular fn para un n dado.
La definición de la recurrencia conduce inmediatamente a una solución recursiva:
public static int F( int n )
{
if( n<= 1)
return n;
else
return F(n-1)+F(n-2);
}
Lamentablemente, este método resulta muy ineficiente. En efecto, si llamamos T(n) al número de operaciones de suma ejecutadas para calcular fn, tenemos que
T(0) = 0 T(1) = 0 T(n) = 1 + T(n-1) + T(n-2)
La siguiente tabla mustra los valores de T(n) para valores pequeños de n:
n 0 1 2 3 4 5 6 7 8 9 10 ... T(n) 0 0 1 2 4 7 12 20 33 54 88 ...
Ejercicio: Demostrar que T(n) = fn+1-1.
Por lo tanto, el tiempo que demora el cálculo de F(n) crece exponencialmente con n, lo cual hace que este método sea inútil excepto para valores muy pequeños de n.
El origen de esta ineficiencia es que la recursividad calcula una y otra vez los mismos valores, porque no guarda memoria de haberlos calculado antes.
Una forma de evitarlo es utilizar un arreglo auxiliar fib[], para anotar los valores ya calculados. Un método general es inicializar los elementos de fib con algún valor especial "nulo". Al llamar a F(n), primero se consulta el valor de fib[n]. Si éste no es "nulo", se retorna el valor almacenado en el arreglo. En caso contrario, se hace el cálculo recursivo y luego se anota en fib[n] el resultado, antes de retornarlo. De esta manera, se asegura que cada valor será calculado recursivamente sólo una vez.
En casos particulares, es posible organizar el cálculo de los valores de modo de poder ir llenando el arreglo en un orden tal que, al llegar a fib[n], ya está garantizado que los valores que se necesitan (fib[n-1] y fib[n-2]) ya hayan sido llenados previamente. En este caso, esto es muy sencillo, y se logra simplemente llenando el arreglo en orden ascendente de subíndices:
fib[0] = 0;
fib[1] = 1;
for( j=2; j<=n; ++j )
fib[j] = fib[j-1]+fib[j-2];
El tiempo total que esto demora es O(n).
Esta idea se llama programación dinámica cuando se la utiliza para resolver problemas de optimización, y veremos algunas aplicaciones importantes de ella a lo largo del curso.
¿Es posible calcular fn más rápido que O(n)? Si bien podría parecer que para calcular fn sería necesario haber calculado todos los valores anteriores, esto no es cierto, y existe un método mucho más eficiente.
Tenemos
fn = fn-1+fn-2 f0 = 0 f1 = 1
Esta es una ecuación de recurrencia de segundo orden, porque fn depende de los dos valores inmediatamente anteriores. Definamos una función auxiliar
gn = fn-1
Con esto, podemos re-escribir la ecuación para fn como un sistema de dos ecuaciones de primer orden:
fn = fn-1+gn-1 gn = fn-1 f1 = 1 g1 = 0
Lo anterior se puede escribir como la ecuación vectorial
fn = A*fn-1
donde
fn = [ fn ] A = [ 1 1 ] [ gn ] [ 1 0 ]
con la condición inicial
f1 = [ 1 ] [ 0 ]
La solución de esta ecuación es
fn = An-1*f1
lo cual puede calcularse en tiempo O(log n) usando el método rápido de elevación a potencia visto anteriormente.
En general, para estudiar la eficiencia de los algoritmos se utilizan funciones discretas, que miden cantidades tales como tiempo de ejecución, memoria utilizada, etc. Estas funciones son discretas porque dependen del tamaño del problema, que se denotará como n. Por ejemplo, n podría representar el número de elementos en un conjunto a ordenar.
Notación: f(n) o bien fn representa el tiempo requerido por un algoritmo dado resolver un problema de tamaño n. También se utiliza T(n) o Tn.
En análisis de algoritmos, cuando n es grande (asintóticamente) lo que importa es el orden de magnitud de la función: cuadrática, lineal, logarítmica, exponencial, etc.. Para n pequeño, la situación puede ser distinta.
Se dice que una función f(n) es O(g(n)) si existe una constante c > 0 y un n0 >= 0 tal que para todo n >= n0 se tiene que f(n) <= cg(n) (cota superior de un algoritmo).
Se dice que una función f(n) es Ω(g(n)) si existe una constante c > 0 y un n0 >= 0 tal que para todo n >= n0 se tiene que f(n) >= cg(n) (cota inferior).
Se dice que una función f(n) es Θ(g(n)) si f(n) = O(g(n)) y f(n) = Ω(g(n)).
Ejemplos:
En orden ascendente: 1/n, 1, log log n, log n, sqrt(n), n, n log n, n1+e, n2, nk, 2n.
Son ecuaciones en que el valor de la función para un n dado se obtiene en función de valores anteriores. Esto permite calcular el valor de la función para cualquier n, a partir de condiciones de borde (o condiciones iniciales)
Ejemplo: Torres de Hanoi
an = 2an-1 + 1 a0 = 0
Ejemplo: Fibonacci
fn = fn-1 + fn-2 f0 = 0 f1 = 1
Consideremos una ecuación de la forma (supuestos: a es una constante mayor que cero y bn es una función conocida):
T(n) = aT(n-1) + bn.
Primero se estudiará el caso más simple cuando a = 1.
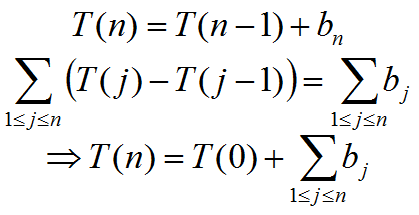
Resolviendo ahora el caso general:
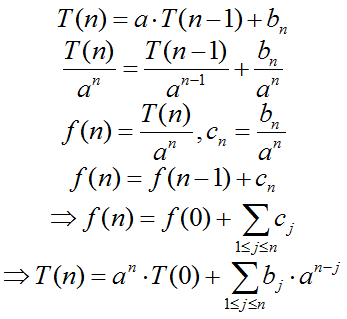
Ejemplo: resolver la ecuación de recurrencia obtenida para el problema de las Torres de Hanoi.
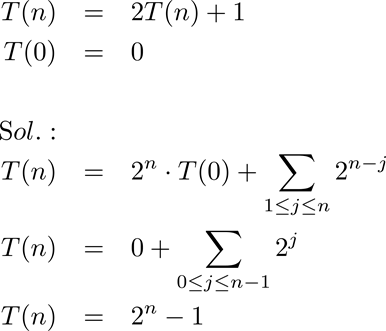
Propuesto: plantee y resuelva la ecuación de recurrencia para la función salida, que resuelve el problema del laberinto.
Estas ecuaciones son de la forma:
fn = Afn-1 + B fn-2 + C fn-3 + ...
con A, B, C, ..., constantes. Este tipo de ecuaciones tienen soluciones exponenciales, de la forma fn = λn.
Ejemplo: Fibonacci.
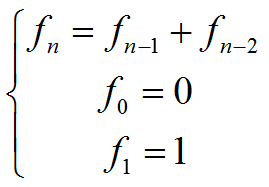
Sustituyendo por su polinomio característico y resolviendo:
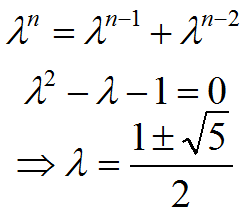
Se define:
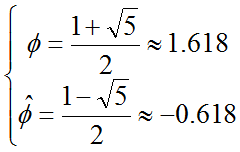
La solución general de la ecuación tiene la forma:
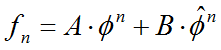
Finalmente, considerando los casos base:
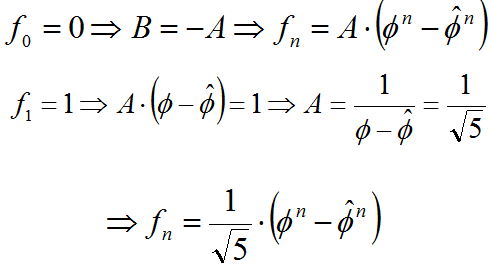
Las ecuaciones de la forma:
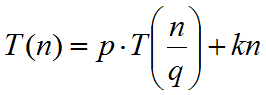
tienen solución:
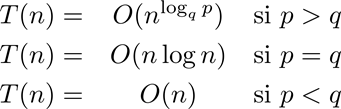
Demostración
"Desenrollando" la ecuación una vez:
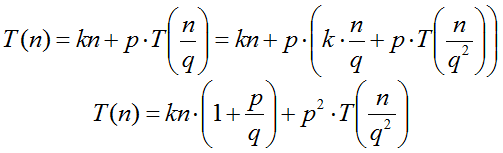
Repitiendo el proceso j - 1 veces se obtiene:
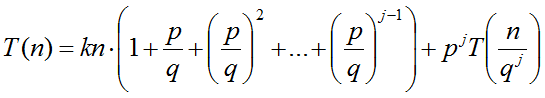
1) Primero se analizará el caso p>q:
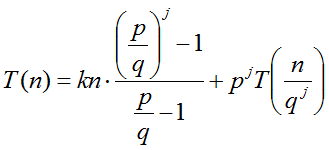
Escogiendo j tal que qj = n (o sea, j = logqn):
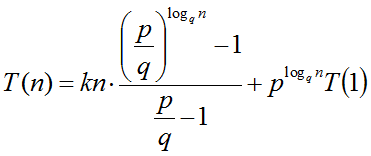
Usando la siguiente igualdad:
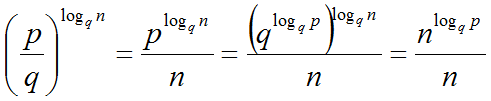
Finalmente, se obtiene:
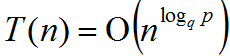
2) Ahora se analizará el caso p=q. Escogiendo j tal que pj = n se obtiene:
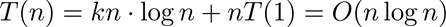
3) Finalmente, se analizará el caso p<q. Escogiendo j tal que qj = n:
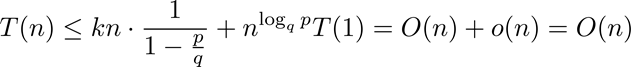
Al igual que en dividir para reinar, la técnica de diseño de programación dinámica divide un problema en varios subproblemas con la misma estructura que el problema original, luego se resuelven dichos subproblemas y finalmente, a partir de éstos, se obtiene la solución al problema original. La diferencia radica en que la programación dinámica se ocupa cuando los subproblemas se repiten, como en el cálculo de los números de Fibonacci. En este caso, en vez de usar recursión para obtener las soluciones a los subproblemas éstas se van tabulando en forma bottom-up, y luego estos resultados son utilizados para resolver subproblemas más grandes. De esta forma, se evita el tener que realizar el mismo llamado recursivo varias veces.
La programación dinámica se ocupa en general para resolver problemas de optimización (maximización o minimización de alguna función objetivo). Estos problemas pueden tener una o varias soluciones óptimas, y el objetivo es encontrar alguna de ellas. Los pasos generales para utilizar programación dinámica en la resolución de un problema son los siguientes:
Estos pasos permiten obtener el valor óptimo de la solución al problema. También es posible ir guardando información extra en cada paso del algoritmo, que luego permita reconstruir el camino realizado para hallar la solución óptima (por ejemplo, para obtener la instancia específica de la solución óptima, y no sólo el valor óptimo de la función objetivo).
Ejemplo: Multiplicación de una secuencia de matrices.
Sea una secuencia de n matrices A1 ... An. Se desea obtener el producto de estas matrices. Para esto, se debe cumplir que dos matrices consecutivas en la secuencia se pueden multiplicar. Es decir, si A y B son matrices consecutivas en la secuencia se cumple que el número de columnas de A es igual al número de filas de B.
El producto se puede obtener multiplicando las matrices en orden de izquierda a derecha. Por ejemplo, si la secuencia tiene tres matrices A, B y C se puede calcular (A * B) * C y obtener el resultado. Sin embargo, esto puede ser ineficiente. Por ejemplo, si A es de dimensiones 100 x 10, B es de dimensiones 10 x 100, y C es de dimensiones 100 x 10, entonces multiplicar (A * B) * C implica calcular (100 * 10 * 100) + (100 * 100 * 10) = 200.000 multiplicaciones (multiplicar dos matrices de p x q y q x r implica calcular p*q*r multiplicaciones escalares). Recordando que la multiplicación de matrices es asociativa, también se puede obtener la solución multiplicando A*(B*C), lo cual tiene un costo de (10 * 100 * 10) + (100 * 10 * 10) = 20.000 multiplicaciones. Esto es diez veces más rápido que la primera parentización. El problema entonces es, dada la secuencia de n matrices, encontrar la parentización óptima que minimice el número de multiplicaciones escalares realizadas para obtener el producto de la secuencia de matrices.
Resolver este problema por fuerza bruta es muy costoso. Se puede demostrar que el número total de parentizaciones distintas a probar está acotado inferiormente por 4n/n3/2.
Solución utilizando recursión
El problema original se puede dividir en subproblemas que tienen la misma estructura que éste. Por ejemplo, si supieramos de antemano que la solución óptima coloca el primer paréntesis en la k-ésima mátriz (es decir, calcula (A1 * ... * Ak) * (Ak+1 * ... * An)), el problema se reduce a encontrar la parentización óptima de las secuencias formadas por A1...Ak y Ak+1...An. Esto es lo que se conoce como subestructura óptima: se puede dividir el problema en subproblemas, y si es posible encontrar las soluciones óptimas a los subproblemas entonces se puede encontrar la solución óptima al problema original.
Propuesto: Demuestre por contradicción que, en el problema de la multiplicación de una cadena de matrices, necesariamente las soluciones a los subproblemas deben ser las óptimas para poder alcanzar el óptimo global.
Con esto ya es posible formular una solución recursiva al problema. Dado que no se conoce de antemano la posición k óptima, se prueban todas las opciones (k = 1, 2, ..., n-1), y el algoritmo retorna aquel k que minimice el número de multiplicaciones escalares. Para resolver los subproblemas se utiliza recursión. En general, si se está resolviendo el intervalo Ai...Aj, se prueba con k = i, i+1, i+2, ..., j-1. Si m[i,j] representa el costo mínimo en multiplicaciones escalares para calcular la multiplicación de la cadena Ai...Aj, para encontrar el óptimo es necesario resolver:
m[i,j] = 0 si i == j
min {m[i,k] + m[k+i,j] + p(i-1)*p(k)*p(j)} si i < j
i <= k < j
Los valores m[i,j] contienen el resultado óptimo para subproblemas del problema original. Para recordar qué valor de k fue el que minimizó el costo, se puede ir almacenando en otra tabla s, en la posición s[i,j]. Esta solución se puede implementar directamente utilizando recursión, pero el algoritmo resultante es muy costoso.
Propuesto: Escriba la ecuación de recurrencia que corresponde al costo del algoritmo recursivo.
La solución a esta ecuación de recurrencia es exponencial, de hecho no es mejor que el costo de la solución por fuerza bruta. ¿Dónde radica la ineficiencia de la solución recursiva? Al igual que en Fibonacci, el problema es que muchos de los llamados recursivos se repiten, es decir, los subproblemas se "traslapan" (overlapping problems). En total, se requiere realizar un número exponencial de llamados recursivos. Sin embargo, el número total de subproblemas distintos es mucho menor que exponencial.
Propuesto: Muestre que el número de subproblemas distintos es O(n2).
Solución utilizando programación dinámica
El hecho que el número de subproblemas distintos es cuadrático (y no exponencial), es una indicación que el problema puede ser resuelto en forma eficiente. En vez de resolver los subproblemas en forma recursiva, se utilizará la estrategia de la programación dinámica, es decir, se tabularán los resultados de los subproblemas, partiendo desde los subproblemas más pequeños, y haciendo los cálculos en forma bottom-up. El siguiente seudocódigo muestra cómo se puede implementar el algoritmo que utiliza programación dinámica:
public static int multiplicacionCadenaMatrices(int[] p, int[][] m, int[][] s)
{
// Matriz Ai tiene dimensiones p[i-1] x p[i] para i = 1..n
// El primer indice para p es 0 y el primer indice para m y s es 1
int n = p.length - 1;
for (int i = 1; i <= n; i++)
{
m[i][i] = 0;
}
for (int l = 2; l <= n; l++)
{
for (int i = 1; i <= n - l + 1; i++)
{
int j = i + l - 1;
m[i][j] = Integer.MAX_VALUE;
for (int k = i; k <= j-1; k++)
{
int q = m[i][k] + m[k+1][j] + p[i-1]*p[k]*p[j];
if (q < m[i][j])
{
m[i][j] = q;
s[i][j] = k;
}
}
}
}
return m[1][n];
}
Finalmente, se puede observar que este algoritmo toma tiempo O(n3), mucho mejor que la solución recursiva, y ocupa espacio O(n2).
Propuesto: Ocupando el resultado obtenido en la tabla s, implemente un algoritmo que calcule el valor de multiplicar la secuencia de matrices utilizando el número óptimo de multiplicaciones escalares.
Nota: también es posible implementar el algoritmo recursivo, pero sólo se hace el llamado la primera vez que se invoca cada recursión y se almacenan los resultados en las tablas correspondientes. Si el valor ya está tabulado, se lee directamente de la tabla, evitando efectuar la recursión para el mismo subproblema más de una vez. A esto se le conoce como memoization.
En problemas de optimización, un algoritmo avaro siempre elige la opción que parece ser la mejor en el momento que la toma. Si bien esto no resuelve todo problema de optimización (puede caer en un óptimo local), hay problemas para los cuales una estrategia avara encuentra siempre el óptimo en forma eficiente.
Ejemplo: Asignación de actividades.
Sea A un conjunto de n actividades a1,...,an que comparten algún recurso importante (y escaso). Cada actividad ai tiene un tiempo de inicio tinii y un tiempo de término tfini, definido por el intervalo semi-abierto [tinii, tfini). Se dice que dos actividades distintas ai y aj son mutuamente compatibles si sus intervalos de tiempo [tinii, tfini) y [tinij, tfinj) no se traslapan. En caso contrario, sólo una de ellas puede llevarse a cabo ya que no es posible que dos actividades compartan simultáneamente el recurso escaso. El problema de asignación de actividades consiste en encontrar un subconjunto maximal A de S que sólo contenga actividades mutuamente compatibles.
Para resolver el problema se utilizará una estrategia avara. Para esto, se supondrá que las actividades están ordenadas temporalmente en forma ascendente de acuerdo al tiempo de término (tfin) de cada actividad. Los tiempos de inicio y término de cada actividad se almacenan en arreglos. El seudocódigo del algoritmo avaro es el siguiente:
asignacionActividadesAvaro(int[] tini, int[] tfin)
{
// Los indices van de 1..n
int n = tini.length;
A = {1} // la primera actividad siempre es parte de la respuesta
int j = 1;
for (int i = 2; i <= n; i++)
{
if tini[i] >= tfin[j]
{
A = A U {i}; // union de conjuntos
j = i;
}
}
return A;
}
La estrategia del algoritmo propuesto es avara, ya que cada vez que es posible se agrega una actividad que es mutuamente compatible con las que ya están en el conjunto A. Este algoritmo toma tiempo O(n) en realizar la asignación de actividades. Falta demostrar que la asignación de actividades realizada por el algoritmo avaro es maximal.
Teorema: el algoritmo implementado en la función asignacionActividadesAvaro produce un conjunto maximal de actividades mutuamente compatibles.
Demostración: Sea A una solución optima para el problema, y suponga que las actividades en A están ordenadas por tiempo de término de cada actividad. Supongamos que la primera actividad en A tiene índice k. Si k = 1, entonces A comienza con una decisión avara. Si k > 1, se define B = A - ak U a1. Dado que A es una solución óptima y las tareas están ordenadas, a1 tiene que ser mutuamente compatible con la segunda actividad en A, por lo que B también es una solución óptima. Es decir, toda solución óptima contiene a la actividad cuyo tiempo de término es el menor de todos, en otras palabras, toda solución óptima comienza con una decisión avara. Por último, la solución A' = A - a1 es una solución óptima para el problema de asignación de tareas para el conjunto S' = {i en S: tinii >= tfin1}, es decir, S' contiene todas las actividades restantes en S que son mutuamente compatibles con a1 (propuesto: demuestre por contradicción que para el conjunto S' no existe una solución óptima B' con más actividades que A'). Esto muestra que el problema de asignación de actividades tiene subestructura óptima: se define un problema más pequeño (S') con la misma estructura que el problema original, cuya solución óptima es parte de la solución al problema original. Por inducción en el número de decisiones tomadas, el tomar la decisión avara en cada subproblema permite encontrar la solución óptima al problema original.
Se estudiarán los siguientes problemas: