Temas:

• Ordenamiento.
• Ordenamiento por selección y reemplazo.
• Análisis del tiempo de ordenamiento por selección y reemplazo.
• Algoritmo de la burbuja.
• Quicksort
• Quicksort con arreglos nativos.

Ordenamiento

El objetivo de estudiar los algoritmos de ordenamiento es doble. Primero, porque permite ejemplificar la importancia del estudio de la eficiencia de los algoritmos, mostrando que no es intuitivo predecir cuanto tiempo de ejecución toman.

Y segundo, porque los computadores pasan típicamente 50% de su tiempo ordenando (de ahí que los españoles y franceses prefieren usar la palabra ordenador en vez de computador). Parece lógico entonces conocer cuáles son los algortimos que se usan para ordenar.

Hace un tiempo atrás era válido un tercer argumento: si en algún momento un programador necesitaba ordenar un arreglo, tenía que programarlo. A partir de 1999, la versión 1.2 de Java incorpora una clase de biblioteca para ordenar datos de manera eficiente.

Ordenamiento por selección y reemplazo

El problema es que trabajar con colas es doblemente ineficiente:

• Porque accesar los elementos de una cola puede ser 50 veces más lento que accesar los elementos de un arreglo nativo.
• Porque utilizar una segunda cola significa que el algoritmo necesita el doble de la memoria.

Entonces se procede a intercambiar los valores de a[0] con a[3]. Ahora, a[0] contiene el valor correcto y por lo tanto, nos olvidamos de él. A continuación, el algoritmo ordena el arreglo desde el índice 1 hasta el 5, ignorando a[0]. Por lo tanto, ubica nuevamente la posición del mínimo entre a[1], a[2], ..., a[5] y lo intercambia con el elemento que se encuentra en a[1] como se indica en el segundo arreglo de la figura. Ahora, a[0] y a[1] contienen los valores correctos. Y así el algoritmo continúa hasta que a[0], a[1], ..., a[5] tengan los valores ordenados.

El algoritmo para ordenar un arreglo a de n elementos es:

Realizar un ciclo de conteo para la variable i, de modo que tome valores desde 0 hasta n-1. En cada iteración:

• Suponer que el arreglo se encuentra ordenado desde a[0] hasta a[i-1].
• Ubicar k>=i, tal que a[k]<=a[j], para todo j en [i,n-1].
• Intercambiar los valores de a[k] y a[i].

  void seleccion(int[ ] a, int n) {
    for (int i= 0; i<n; i++) {
      // Buscamos la posicion del minimo en a[i], a[i+1], ..., a[n-1]
      int k= i;
      for (int j= i+1; j<n; j++) {
        if (a[j]<a[k])
          k= j;
      }
      // intercambiamos a[i] con a[k]
      int aux= a[i];
      a[i]= a[k];
      a[k]= aux;
    }
  }

Se podría introducir una instrucción if para que no se realice el intercambio cuando k==i, pero esto sería menos eficiente que realizar el intercambio aunque no sirva. En efecto, en algunos casos el if permitiría ahorrar un intercambio, pero en la mayoría de los casos, el if no serviría y sería un sobrecosto que excedería con creces lo ahorrado cuando sí sirve.

Análisis del tiempo de ordenamiento por selección y reemplazo

Desarrollando esta inecuación se llega a:

Con A, B y C constantes a determinar. Por lo tanto es fácil probar que:

De la misma forma se puede probar que en el mejor caso y en el caso promedio, el algoritmo también es O(n^2). Por lo tanto:

• Mejor caso: O(n^2)
• Peor caso: O(n^2)
• Caso promedio: O(n^2)

Es fácil probar que el algoritmo basado en colas también es O(n^2) cuando las operaciones agregar y extraer en la cola toman tiempo constante. Esto no es necesariamente cierto porque depende de cómo esté implementada la clase Queue. En todo caso sí es cierto si la cola se implementa con arreglos nativos o con las listas enlazadas que veremos pronto.

La siguiente es una comparación empírica de los tiempos de ejecución de ambos algoritmos:

Se puede observar que el uso de arreglos nativos es unas 50 veces más eficiente que la cola. Sin embargo, el algoritmo de ordenamiento por selección y reemplazo sigue siendo O(n^2) y por lo tanto es ineficiente.

En efecto, si consideramos el problema de la clase pasada en que se necesitaba ordenar para luego realizar búsquedas eficientes, esta solución no sirve, porque el ordenamiento tiene un sobrecosto que excede las ganancias de la búsqueda binaria.

Algoritmo de la burbuja

La idea consiste en realizar varios recorridos secuenciales en el arreglo intercambiando los elementos adyacentes que estén desordenados. Como se muestra en la siguiente figura, en la primera iteración se lleva el máximo a su posición definitiva al final del arreglo:

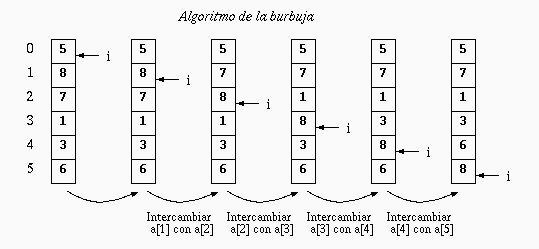
En la segunda iteración se lleva el segundo máximo a su posición definitiva. Y así continúa hasta ordenar todo el arreglo. Observe que si en un recorrido secuencial no se intercambia ningún elemento, el arreglo está ordenado y se puede concluir. El código es entonces:

  void burbuja(int[ ] a, int n) {
    int iult= n-1;
    boolean cambio= true;
    while (cambio) {
      cambio= false;
      for (int i= 0; i<iult; i++) {
        if (a[i]>a[i+1]) {
          // intercambiar
          int aux= a[i];
          a[i]= a[i+1];
          a[i+1]= aux;
          cambio= true;
        }
      }
      iult--;
    }
  }

Análisis:

• Mejor caso: O(n)
• Peor caso: O(n^2)
• Caso promedio: O(n^2)

Comparación con selección y reemplazo:

Al ordenar arreglos completamente desordenados, el algoritmo de la burbuja toma el doble de tiempo que selección y reemplazo. Sin embargo, puede llegar a ser mucho más eficiente con arreglos semi-ordenados.

Quicksort

Primero veremos una versión que ordena una cola de enteros y luego pasaremos a la versión que ordena arreglos de enteros. La versión que trabaja con colas de enteros es muy simple y se explica de la siguiente forma:

Caso base:

Si cola esta vacía, se puede considerar que está ordenada, de modo que se retorna de inmediato, sin hacer nada.

Invocaciones recursivas:

• Extraiga un elemento de la cola inicial. Este elemento será considerado el pivote.

• Construya dos nuevas colas vacías. La primera cola se usará para almacenar elementos menores que el pivote, la segunda para elementos mayores o iguales al pivote.

• Extraiga uno a uno los elementos que quedan en la cola inicial. Los elementos que son menores que el pivote, agréguelos al final de la cola de menores. Los elementos que son mayores o iguales, colóquelos en la cola de los mayores o iguales.

• Ahora la cola inicial está vacía, pero sus elementos están almacenado en: la variable pivote, la cola con los elementos menores que el pivote y la cola con los elementos mayores o iguales que el pivote.

• Ordene recursivamente la cola de menores. Este problema es obligatoriamente más simple que el problema inicial, porque esta cola contiene menos elementos que la cola inicial.

• Ordene recursivamente la cola de mayores o iguales. Esta cola no contiene el pivote, y por lo tanto es de menor tamaño que la cola inicial.

• Transfiera a la cola inicial: los elementos de la cola de menores, el pivote y los elementos de la cola de mayores, en ese orden.

• Ahora la cola inicial se encuentra ordenada!

  void quicksort(Queue cola) {
    // Caso base
    if (cola.isEmpty())
      return;
    // Caso recursivo
    int pivot= cola.getInt(); // La cola no esta vacía
    Queue menores= new Queue(); // Una cola para los menores que x
    Queue mayores= new Queue(); // Una cola para los mayores que x
    // Particionamiento
    while (!cola.isEmpty()) {
      int x= cola.getInt();
      if (x>pivot)
        mayores.put(x);
      else
        menores.put(x);
    }
    quicksort(menores); // Se ordenan los menores recursivamente
    quicksort(mayores); // Se ordenan los mayores recursivamente
    // Se regresan los valores a la cola inicial
    while (!menores.isEmpty())
      cola.put(menores.getInt());
    cola.put(pivot);
    while (!mayores.isEmpty())
      cola.put(mayores.getInt());
  }

Suponiendo que agregar y extraer elementos de la cola toma tiempo constante, el análisis es el siguiente:

• Mejor caso: ?
• Peor caso: O(n^2)
• Caso promedio: O(n log n)!

A continuación veremos que la práctica ratifica la teoría.

Comparación de algoritmos

Observe que para ordenar conjuntos de pocos elementos, quicksort con colas el muchos más lento que selección con arreglos nativos. Sin embargo, con conjuntos de 2000 elementos, ambos se demoran lo mismo. Pero sobretodo, para arreglos de gran tamaño, quicksort con colas es más rápido.

Sin embargo, quicksort con colas todavía no es lo suficientemente rápido. Quicksort con arreglos nativos es aún más rápido. De hecho, es el algoritmo de ordenamiento más eficiente conocido.

Conclusión esencial Para expresar la eficiencia de un algoritmo se usa la notación O(f(n)). Supongamos que dos algoritmos F y G toman tiempo O(f(n)) y O(g(n)) respectivamente. Esto significa que para algún k se tiene:

Si f(n) crece más lentamente que g(n), entonces F es más eficiente que G, sin importar las constantes CF y CG. Por muy grande que sea la constante de F con respecto a la constante de G, tarde o temprano existirá un n a partir del cual F será más rápido que G.

Quicksort con arreglos nativos

    void quicksort(int[] a, int imin, int imax) {
      if (imin>=imax)
        return;
      int k= particionar(a, imin, imax);
      quicksort(a, imin, k-1);
      quicksort(a, k+1, imax);
    }

Finalmente, la función particionar debe entregar la posición en que queda el pivote. Esta es la parte más complicada de quicksort, porque hay que hacerlo sin utilizar un arreglo auxiliar. Además el valor de k es desconocido.

A continuación veremos una versión de particionar que elige como pivote el primer elemento en el intervalo que se va a ordenar (es decir el pivote es a[imin]). Luego, hace variar j desde imin+1 hasta imax. La situación inicial del arreglo es la que se indica en el primer arreglo de la figura. El segundo arreglo muestra la situación antes de comenzar una iteración para un valor determinado de j. Se observa que todos los elementos de a[imin+1] hasta a[k] deben ser menores que el pivote y desde a[k+1] hasta a[j-1] deben ser mayores o iguales al pivote:

Por lo tanto, en cada iteración se compara a[j] con el pivote. Si es menor, se hace crecer k en una posición y se intercambia el elemento k con el elemento j para que se cumpla la situación intermedia en la siguiente iteración.

El tercer arreglo en la figura indica la situación al salir del ciclo. Se observa que el arreglo está prácticamente particionado. Sólo falta colocar el pivote en la k-ésima posición. Esto se logra intercambiando el primer elemento con la k-ésima posición.

  int particionar(int[] a, int imin, int imax) {
    int ipiv= imin;
    int k= imin;
    int j= k+1;
    while (j<=imax) {
      if (a[j]<a[ipiv] ) {
        k= k+1;
        intercambiar(a, k, j);
      }
      j= j+1;
    }
    intercambiar(a, k, ipiv);
    return k;
  }